はじめに
数学パズル(その1)の続編です。
今回は折紙パズルが多くなりました。
皆様、是非とも自分で考えて楽しんで下さい。
問題1
別の折紙パズルに挑戦します。
[問題]
正方形を2本の直線で切り離し、平行移動して並べ替えて正方形と同じ面積の長方形にするには、どうすればいいのか?
ただし、正方形の対角線≧作る長方形の長辺>正方形の一辺とします。
[出典]
文献[1]の7ページ
[コメント]
ちょっとだけ考えました。
2本の直線を見つけるだけなので簡単と思えましたが、実体は難しそうです。
腰を落ち着けて取り組みたい問題です。
閃いて、自力で解くことができました。
ヒントの画像を置いておきます。



問題2
更なる折紙パズルを考えます。
[問題]
長方形を2本の直線で切り離し、平行移動して並べ替えて長方形と同じ面積の正方形にするには、どうすればいいのか?
ただし2回のカットで正方形ができるのは、長辺<短辺×2の長方形用紙です。
[出典]
文献[1]の8ページ
[コメント]
超難問の気配を感じます。
まずはコピー用紙(白銀矩形)で考えると良いような気がします。
7ページの変形を逆に行えば、長方形から長方形を作成できそう。
さっぱり分からないので解答を見ちゃいました。
ヒントの画像を置いておきます。



カットするのは、2本の赤の線分です。
アルゴリズムの正当性は「2本の赤の線分が同じ長さかつ垂直に交わる」で保証されます。
この正当性の証明も自力では無理でした。

問題3
次は軽めの問題にします。
でも面白いと思います。
[問題]
コピー用紙(白銀矩形)を用いてタンジェント22.5°を求めよ。
白銀矩形とは長辺と短辺の比がルート2の長方形である。
[出典]
文献[2]
[コメント]
この問題は自力で解けました。嬉しい。
ヒントの画像を置いておきます。
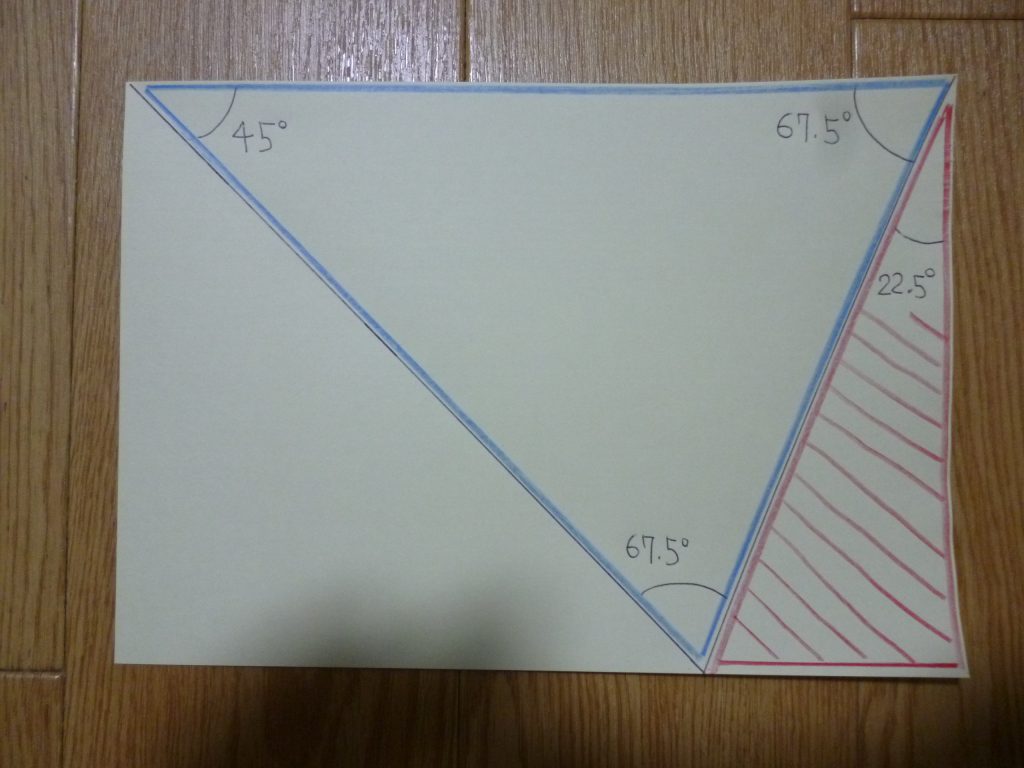
ポイントは、青の3角形が2等辺3角形になることです。
赤の3角形に注目すると、タンジェント22.5°がルート2マイナス1となります。
問題4
ネットで凄いウワサをキャッチしました。
ルート2の無理数性を折紙で証明できるらしいです。
真偽を確かめたいと思います。
[問題]
折紙を用いて、ルート2が無理数であることを証明せよ.
[出典]
文献[3]の102ページ
[コメント]
ウワサは本当でした.
証明のポイントと画像をメモしておきます.
ルート2を有理数a/bと仮定する.
a, bはそれぞれ自然数である.
画像の通り折紙をする.


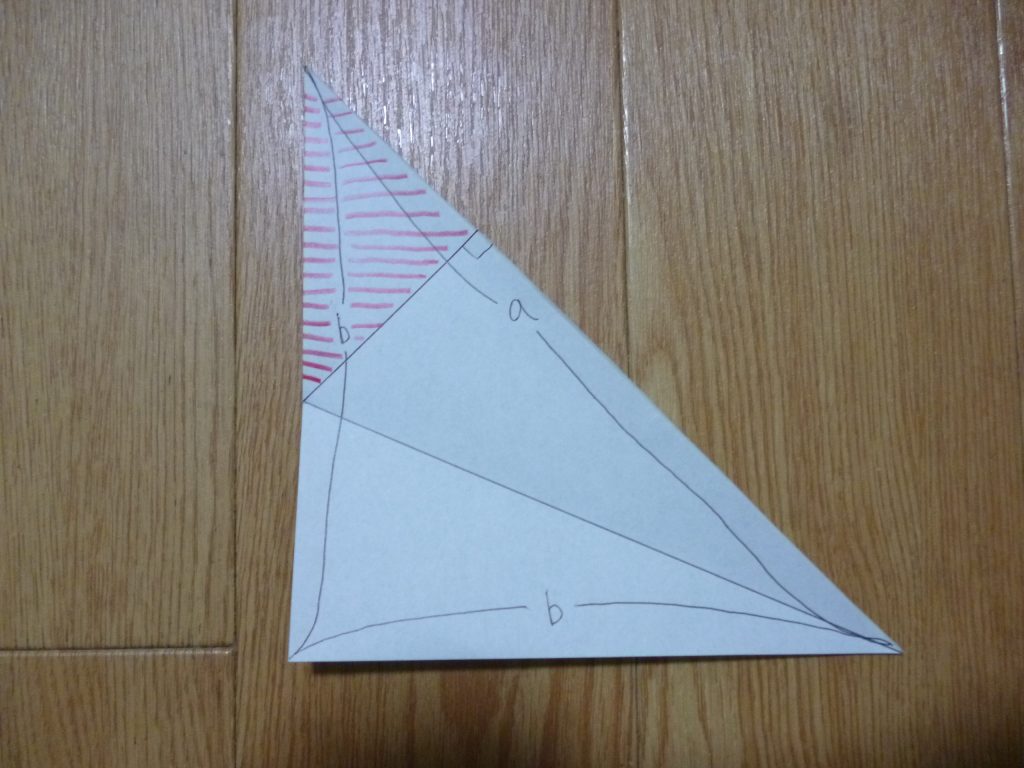
赤の3角形は元の3角形と相似なので,
ルート2 = (2b – a)/(a – b)となる.
1 < a/b < 2より, a > 2b-a > 0かつ b > a-b > 0が成立する.
よって, ルート2をa/b → (2b – a)/(a – b)とする代数的操作は有限回しか繰り返せない.
その一方で元の3角形から赤の3角形を折紙で構成する幾何学的操作は無制限に何回でも繰り返せる.
代数的操作と幾何学的操作の間に矛盾が生じる.
よってルート2は無理数である.
問題5
次は錯視を用いたパズルです.
[問題]
以下のサイトの画像にある立体図形をコピー用紙1枚で作成せよ.
https://www.cutoutfoldup.com/1102-impossible-flap-.php

[出典]
文献[4]の72ページ
[コメント]
うーん、悩ましいです。どうやったらこんな物を作れるんだ?
実際に工作をすると5分で解けました。

3本の赤の線分を切ります.
そして、横線を回転軸として紙を少しひねると完成です.
画像を見ているだけだと全く分かりませんが、実際に工作してみるとすぐ理解できます。

参考文献
[1] 阿部恒. (2012). すごいぞ折り紙入門編: 折り紙の発想で幾何を楽しむ. 日本評論社.
[2] Bogomolny, A. (2018). Cut The Knot, Tangent of 22.5° – Proof Without Words.
https://www.cut-the-knot.org/pythagoras/Tangent225.shtml
[3] Toth, G. (2021). Elements of Mathematics: A Problem-Centered Approach to History and Foundations. Springer International Publishing.
[4] Jackson, P. (2013). Cut & Fold Techniques for Promotional Materials. Laurence King Publishing.
作成: 藤原大樹
更新: 2024年2月22日
