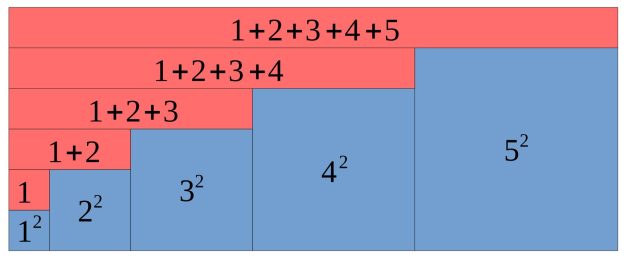
公式
\[
1^2+2^2+3^2+ \dots + n^2 = \frac{1}{6}n(n+1)(2n+1)
\]
を4通りの方法で証明しました。
高校数学は奥が深いです。
そして更に、公式
\[
1^3+2^3+3^3+ \dots + n^3 = \frac{1}{4}n^2(n+1)^2
\]
を3通りの方法で証明しました。
作成: 藤原大樹
更新: 2022年8月17日
高校数学を復習しています。
公式
\[
1+2+3+ \dots + n = \frac{1}{2}n(n+1)
\]
を3通りの方法で証明しました。
作成: 藤原大樹
更新: 2022年8月9日
抜群に面白い入試問題を見つけたので、紹介します。ネイピア数$e$が無理数であること及び$e = \sum_{k=0}^\infty \frac{1}{k!}$であることの2つを証明します。入試問題なので高校数学しか使いませんし、問題の難易度はセンター試験レベルです。模範解答と問題解説をPDFファイルにまとめました。よかったら見て下さい。
作成: 藤原大樹
更新: 2022年8月6日
京アカオンライン輪読会では、次に和辻哲郎『風土―人間学的考察』（岩波文庫）の輪読会を、8月17日（水）20：00より始めます。前提知識一切不要、予習なしでその場で輪読し、議論します。試しに一回だけの参加、ときどきの参加もばっちりOK。どなたでも参加できます。参加ご希望の方は、各自で本をご用意下さい。お問合わせはkyotoacademeia@gmail.comまで。多数のご参加をお待ちしています！
https://www.iwanami.co.jp/book/b270343.html
歎異抄オンライン輪読会は本日（8月3日）で終了しました。活発な議論もあり、新しい角度から歎異抄を読み直すことができました。ご参加下さった皆さま、どうもありがとうございました。
京アカオンライン輪読会では、次に和辻哲郎『風土』（岩波文庫）を読む予定です。詳細は改めてご連絡いたします。