高校数学だけでバーゼル問題を解きました.
その様子をPDFにまとめたので、良かったら見て下さい.

作成: 藤原大樹
更新: 2024年2月28日
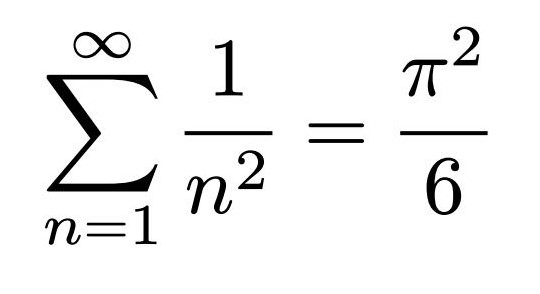

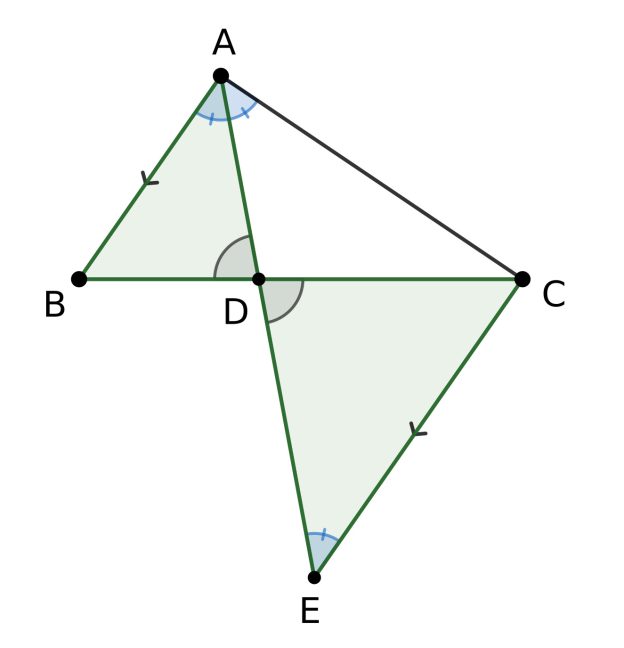
今日は平面幾何学の”角の二等分線定理”を勉強しました。
この定理は、小学生でも知っている大変有名な定理です。
しかしながら、お恥ずかしい話ですが、今日産まれて初めて証明を知りました。
そこで理解を深めるために3つの証明をPDFファイルに要約しました。
どの証明も個性的でイラストを見ているだけで胸が躍ります。

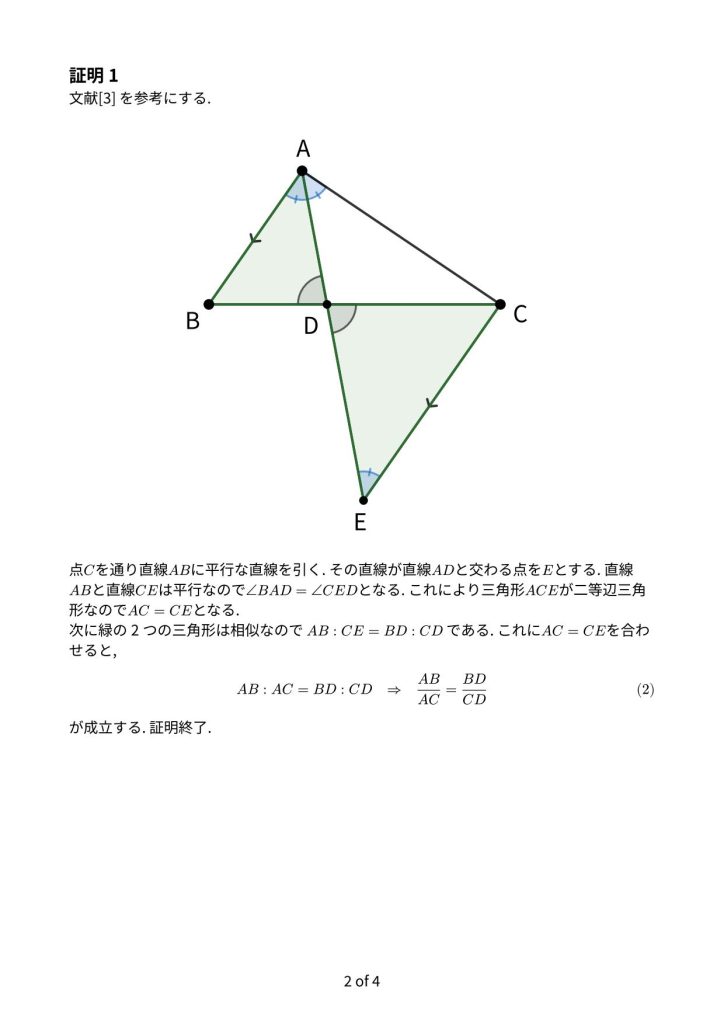
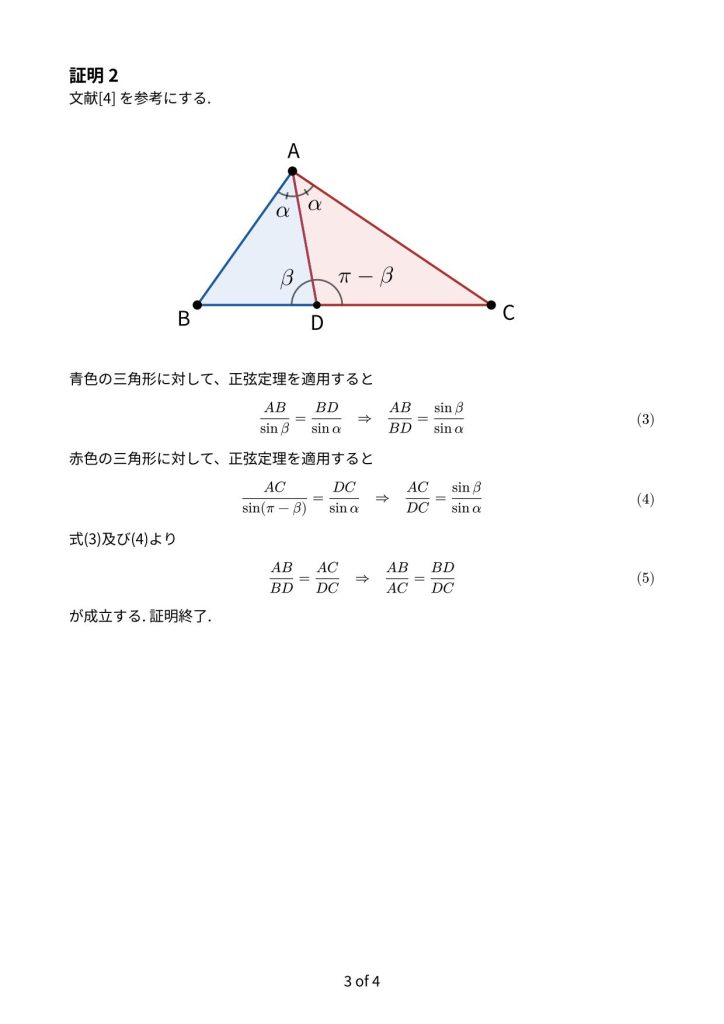

作成: 藤原大樹
更新: 2024年2月24日

数学パズル(その1)の続編です。
今回は折紙パズルが多くなりました。
皆様、是非とも自分で考えて楽しんで下さい。
別の折紙パズルに挑戦します。
[問題]
正方形を2本の直線で切り離し、平行移動して並べ替えて正方形と同じ面積の長方形にするには、どうすればいいのか?
ただし、正方形の対角線≧作る長方形の長辺>正方形の一辺とします。
[出典]
文献[1]の7ページ
[コメント]
ちょっとだけ考えました。
2本の直線を見つけるだけなので簡単と思えましたが、実体は難しそうです。
腰を落ち着けて取り組みたい問題です。
閃いて、自力で解くことができました。
ヒントの画像を置いておきます。



更なる折紙パズルを考えます。
[問題]
長方形を2本の直線で切り離し、平行移動して並べ替えて長方形と同じ面積の正方形にするには、どうすればいいのか?
ただし2回のカットで正方形ができるのは、長辺<短辺×2の長方形用紙です。
[出典]
文献[1]の8ページ
[コメント]
超難問の気配を感じます。
まずはコピー用紙(白銀矩形)で考えると良いような気がします。
7ページの変形を逆に行えば、長方形から長方形を作成できそう。
さっぱり分からないので解答を見ちゃいました。
ヒントの画像を置いておきます。



カットするのは、2本の赤の線分です。
アルゴリズムの正当性は「2本の赤の線分が同じ長さかつ垂直に交わる」で保証されます。
この正当性の証明も自力では無理でした。

次は軽めの問題にします。
でも面白いと思います。
[問題]
コピー用紙(白銀矩形)を用いてタンジェント22.5°を求めよ。
白銀矩形とは長辺と短辺の比がルート2の長方形である。
[出典]
文献[2]
[コメント]
この問題は自力で解けました。嬉しい。
ヒントの画像を置いておきます。
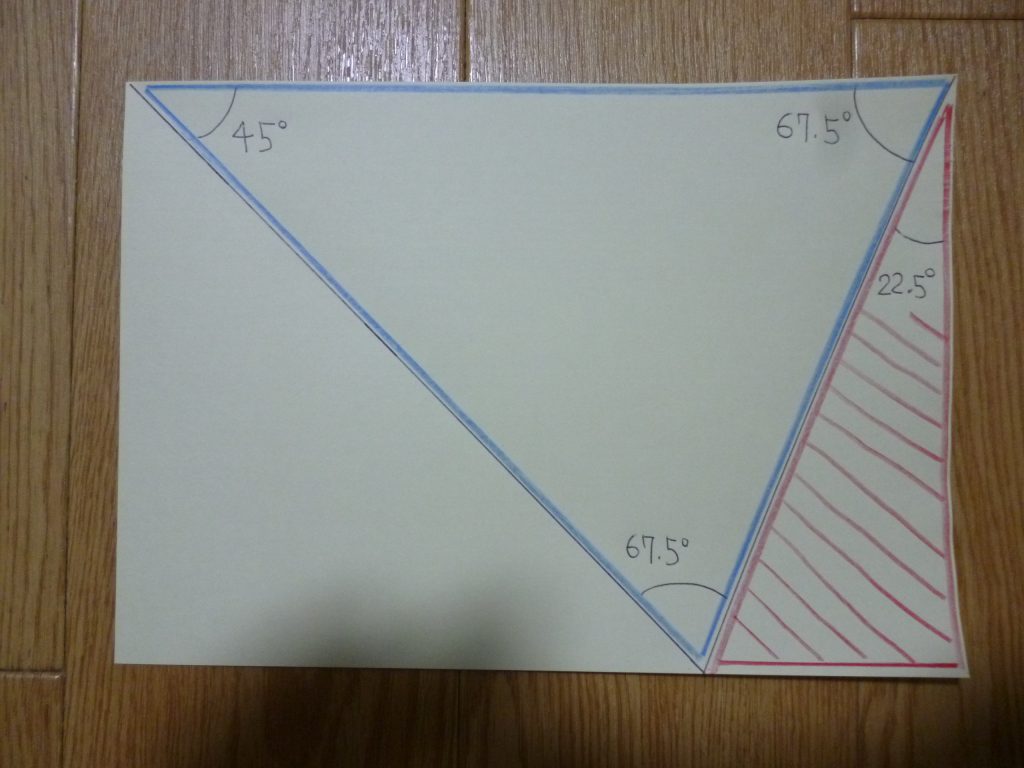
ポイントは、青の3角形が2等辺3角形になることです。
赤の3角形に注目すると、タンジェント22.5°がルート2マイナス1となります。
ネットで凄いウワサをキャッチしました。
ルート2の無理数性を折紙で証明できるらしいです。
真偽を確かめたいと思います。
[問題]
折紙を用いて、ルート2が無理数であることを証明せよ.
[出典]
文献[3]の102ページ
[コメント]
ウワサは本当でした.
証明のポイントと画像をメモしておきます.
ルート2を有理数a/bと仮定する.
a, bはそれぞれ自然数である.
画像の通り折紙をする.


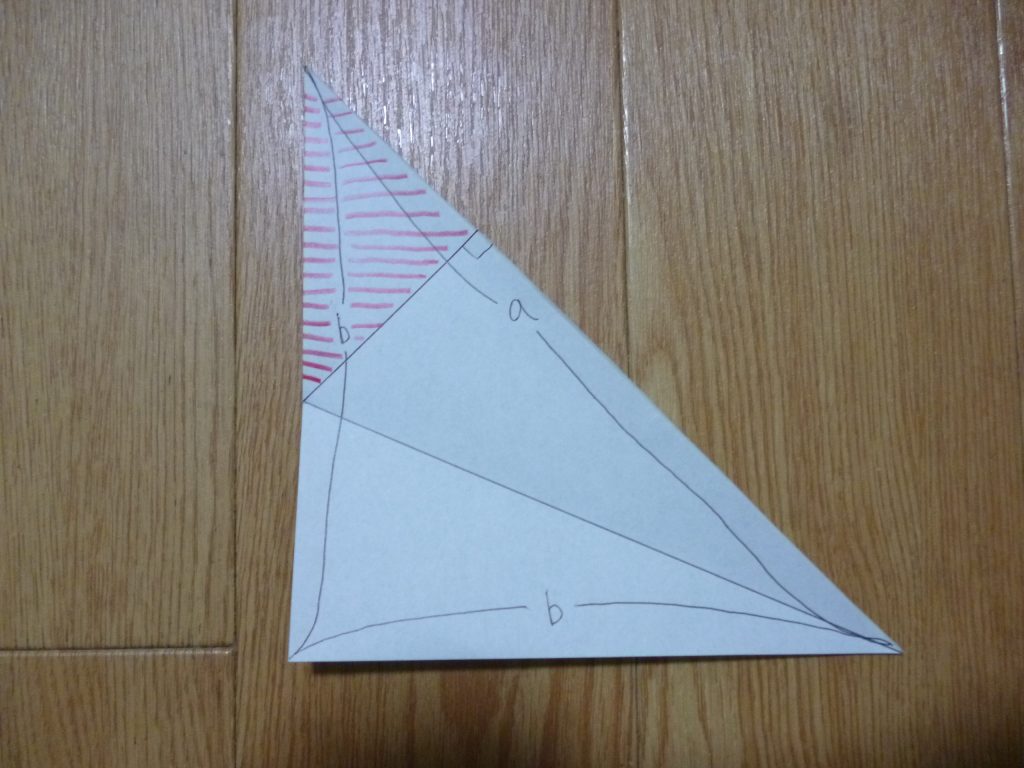
赤の3角形は元の3角形と相似なので,
ルート2 = (2b – a)/(a – b)となる.
1 < a/b < 2より, a > 2b-a > 0かつ b > a-b > 0が成立する.
よって, ルート2をa/b → (2b – a)/(a – b)とする代数的操作は有限回しか繰り返せない.
その一方で元の3角形から赤の3角形を折紙で構成する幾何学的操作は無制限に何回でも繰り返せる.
代数的操作と幾何学的操作の間に矛盾が生じる.
よってルート2は無理数である.
次は錯視を用いたパズルです.
[問題]
以下のサイトの画像にある立体図形をコピー用紙1枚で作成せよ.
https://www.cutoutfoldup.com/1102-impossible-flap-.php

[出典]
文献[4]の72ページ
[コメント]
うーん、悩ましいです。どうやったらこんな物を作れるんだ?
実際に工作をすると5分で解けました。

3本の赤の線分を切ります.
そして、横線を回転軸として紙を少しひねると完成です.
画像を見ているだけだと全く分かりませんが、実際に工作してみるとすぐ理解できます。

[1] 阿部恒. (2012). すごいぞ折り紙入門編: 折り紙の発想で幾何を楽しむ. 日本評論社.
[2] Bogomolny, A. (2018). Cut The Knot, Tangent of 22.5° – Proof Without Words.
https://www.cut-the-knot.org/pythagoras/Tangent225.shtml
[3] Toth, G. (2021). Elements of Mathematics: A Problem-Centered Approach to History and Foundations. Springer International Publishing.
[4] Jackson, P. (2013). Cut & Fold Techniques for Promotional Materials. Laurence King Publishing.
作成: 藤原大樹
更新: 2024年2月22日
最近、数学パズルにハマっています。楽しいです。その奮闘状況を京アカTwitterで報告していました。皆様からいいねをたくさん頂き、予想外に反響が大きかったです。そのお陰でやる気が高まりました。皆様ありがとうございます。その一方で情報が溜まってくるにつれTwitterでは見ずらくなってきました。なので、これまでの情報をブログに整理します。
今回はとっておきの5題を紹介します。必要となる予備知識は中学生レベルなので、文系の皆様も楽しめると思います。解答は著作権の関係ですべてを記載することはできません。当ブログでは解答のエッセンスとなるヒントだけ示します。詳細な解答を知りたい方は申し訳ないですが、参考文献に当たって下さい。
あと、年明けからオンライン自習室を再開しているのですが、誰も来てくれません。寂しいです。誰か来てくれると嬉しいです。
[問題]
Show how to cut a cube to form a regular hexagon.
立方体から1枚の正6角形を切り出す方法は?
[出典]
文献[3]の問題3.4
[コメント]
理解を深めるために折紙で模型を作りました。
立方体の断面が確かに正6角形になっています。



[問題]
The famous number φ is called the golden ratio and is usually associated with a regular pentagon. Show how to construct φ using just an equilateral triangle.
黄金比φは正5角形に通常関連づけられる。黄金比φを1つの正3角形だけから構成する方法は?
[出典]
文献[3]の問題3.9
[コメント]
分からないので解答を見ちゃいました。
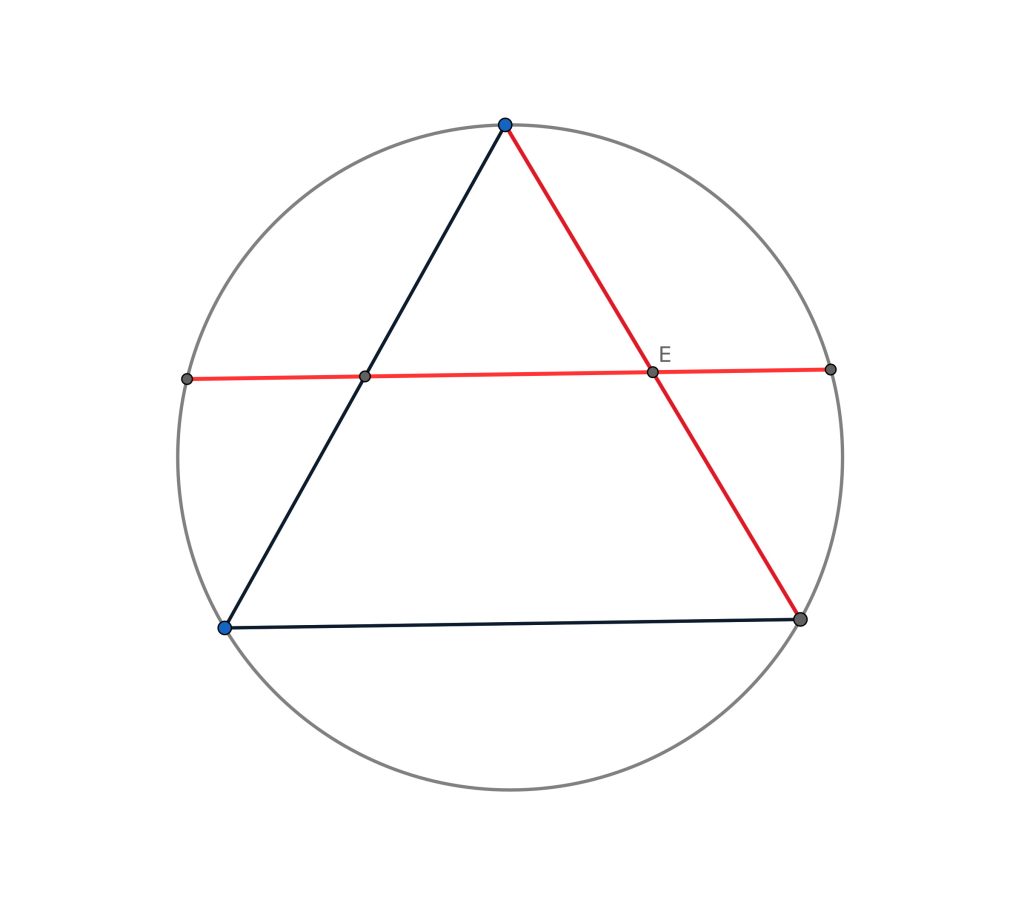
大ヒントは次の画像です。
2本の赤の線分に対してThe Intersecting Chords Theoremを適用すると?
[問題]
Show that the sum of the angles of a plane triangle is 180°.
平面において3角形の内角の和が180度であることを示せ.
[出典]
文献[3]の問題3.8
[コメント]
普通の証明は以下の図だと思います。
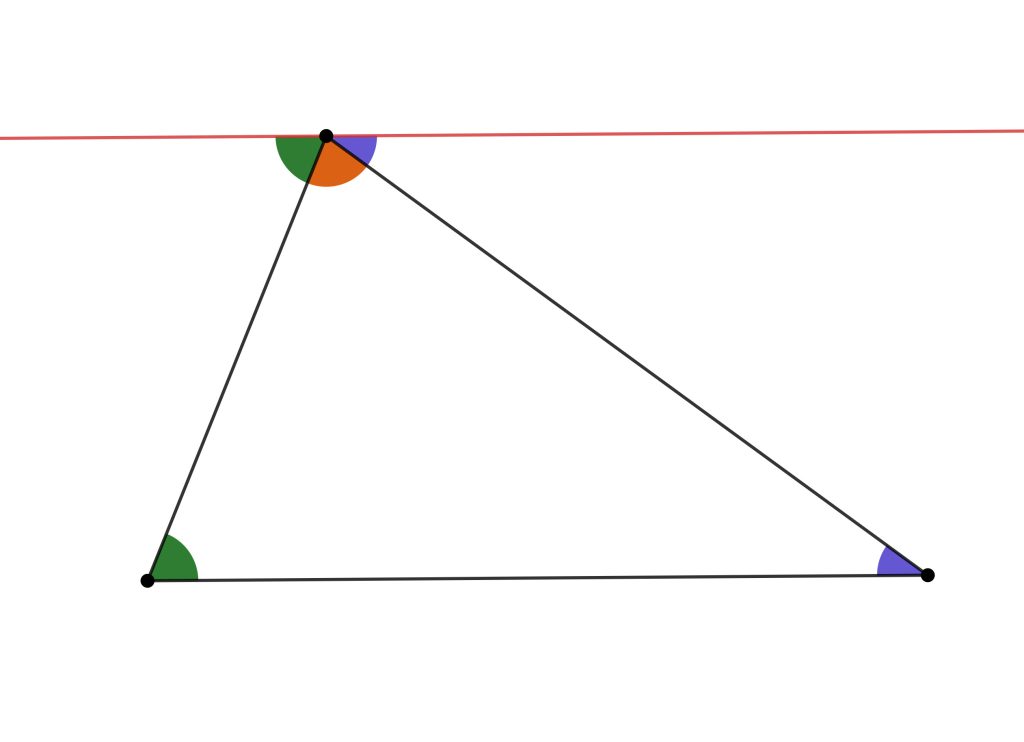
文献[3]の解答は、ピタゴラスによる普通の証明だけでした。
しかし、文献[4]では4つの証明が紹介されています。非常に勉強になりそうです。
[問題]
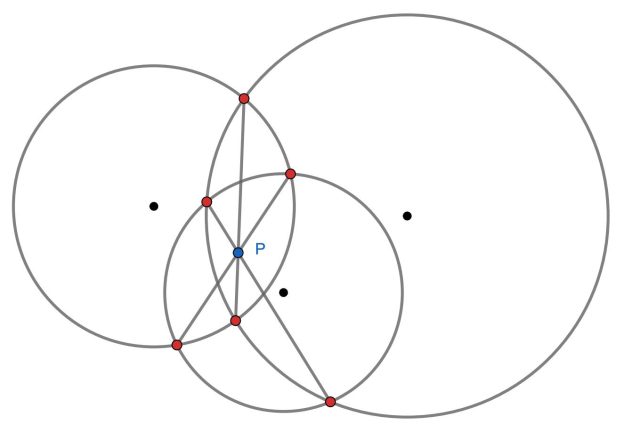
Each of three circles in the plane intersects the other two in exactly two points, giving exactly six distinct intersection points in all. Show that the common chords of each two circles are concurrent, that is, meet at a single point.
言葉で理解するよりも図で示します。
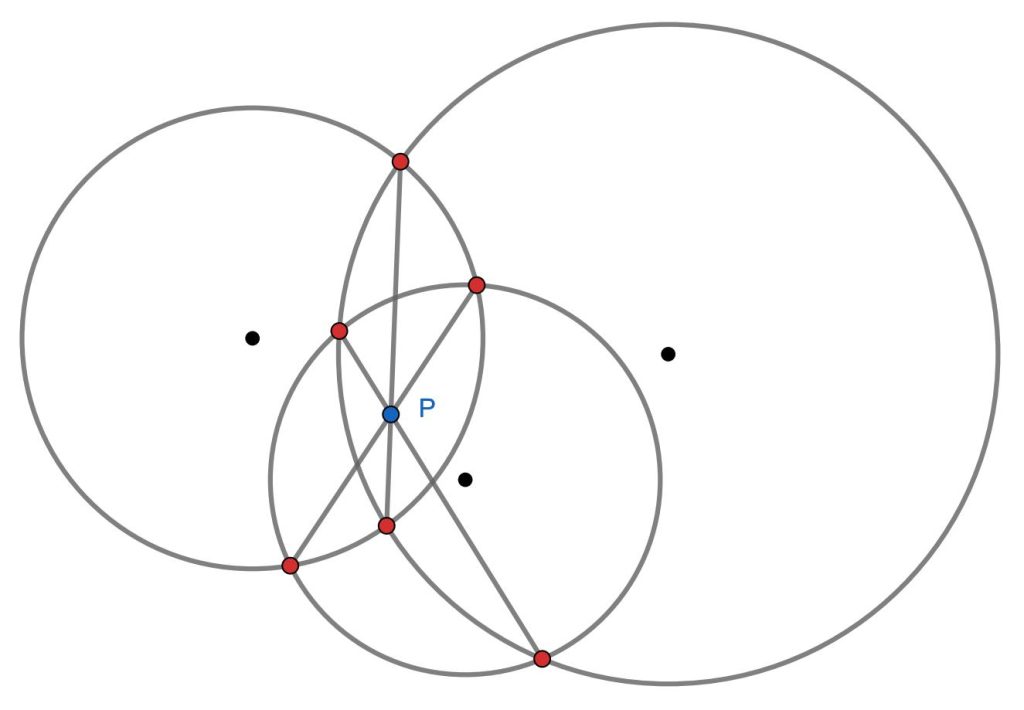
[出典]
文献[3]の問題3.3
[コメント]
この問題は文献[2]の264ページで見かけたことがあります. 証明が同じかどうか気になります. まずは文献[2]を復習します.
文献[2]ではthe intersecting chords theorem(方べきの定理)を用いた幾何学的な証明が与えられていました。一方、文献[3]の証明は代数的でした。代数的な証明のヒントをメモしておきます。

[背景]
折紙でピタゴラスの定理(三平方の定理)を証明できるという情報をキャッチしました。ホントかどうか確かめるために文献[1]の13ページを読みます。
[問題]
正方形を切り離し、平行移動して並び替えて2つの面積の異なる正方形にするには、どうすればいいのか?
[コメント]
初見では分かりませんが、じっくり考えます。
分からなかったので解答を見ました。自分では絶対発見できません。皆様のために、ヒントの画像を置いておきます。



青色の直角三角形に関して、ピタゴラスの定理が成立します。
その理由は、元の正方形の面積と変形後の図形である2つの正方形の合計面積を比較すると同じだからです。
面白い証明です。今回初めて知りました。
[1] 阿部恒. (2012). すごいぞ折り紙入門編: 折り紙の発想で幾何を楽しむ. 日本評論社.
[2] Acheson,D. (2020). The Wonder Book of Geometry: A Mathematical Story. OUP Oxford.
[3] MacHale,D. (2023). Lateral Solutions to Mathematical Problems. CRC Press.
[4] Bogomolny,A. (2018). Cut The Knot, Angles in Triangle Add to 180°.
https://www.cut-the-knot.org/triangle/pythpar/AnglesInTriangle.shtml
作成: 藤原大樹
更新: 2024年2月17日