公式
\[
1^2+2^2+3^2+ \dots + n^2 = \frac{1}{6}n(n+1)(2n+1)
\]
を4通りの方法で証明しました。
高校数学は奥が深いです。
そして更に、公式
\[
1^3+2^3+3^3+ \dots + n^3 = \frac{1}{4}n^2(n+1)^2
\]
を3通りの方法で証明しました。
作成: 藤原大樹
更新: 2022年8月17日
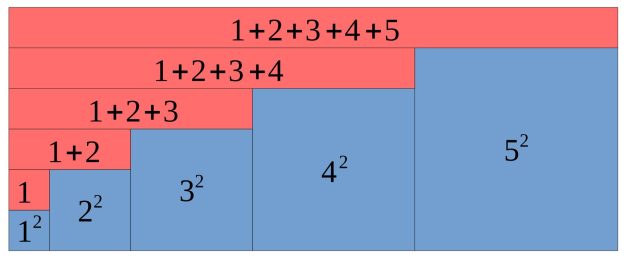
公式
\[
1^2+2^2+3^2+ \dots + n^2 = \frac{1}{6}n(n+1)(2n+1)
\]
を4通りの方法で証明しました。
高校数学は奥が深いです。
そして更に、公式
\[
1^3+2^3+3^3+ \dots + n^3 = \frac{1}{4}n^2(n+1)^2
\]
を3通りの方法で証明しました。
作成: 藤原大樹
更新: 2022年8月17日