浅野直樹

先日 「大学入学共通テスト（仮称）」記述式問題のモデル問題例が公表されました。数学の解説をアップします。PDFとtexファイルも用意しました。texはemathを活用しています。

nyushi_kaisetu（PDF）

nyushi_kaisetu（tex）

＜目次＞
モデル問題例3
$[1]$
$(1)$
$(2)$
$(3)$

[2]
$(1)$
$(2)$
$(3)$
$(4)$

モデル問題例4
$[1]$
$(1)$
$(2)$

$[1]$

$(1)$
$(\rm i)$
$OE=\frac53$である。
$AE=\frac13$なので、$BF=2AE=\frac23$である。
$OF=OB+BF$
$=2+\frac23$
$=\frac83$
よって、$\bigtriangleup{FOE}=\frac12\cdot{OE}\cdot{OF}$
$=\frac12\cdot\frac53\cdot\frac83$
$=\frac{20}9$
$S=4\bigtriangleup{FOE}$
$=4\cdot\frac{20}9$
$\fbox{$=\frac{80}9$}$

$(\rm ii)$
$AE=x$とすると、$0\leqq{x}<2$である。
$(\rm i)$と同様に考えて
$OE=2-x, \ OF=2+2x$より
$S=4\cdot\frac12(2-x)(2+2x)$
$=-4x^2+4x+8$
$=-4(x-\frac12)^2+9$
これは頂点が$(\frac12, 9)$で上に凸の2次関数である。

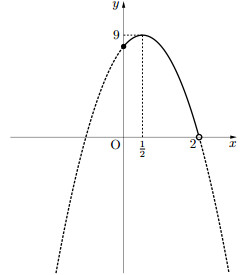
図より、$0\leqq{x}<2$の範囲では$\fbox{$0<S\leqq9$}$となる。

$(2)$
$T=4\cdot\frac12\cdot2\cdot2$
$=8$
EがOA上にあるときは、$(1)(\rm ii)$より
$-4x^2+4x+8=8$を解いて
$x=0, 1$
EがAと一致しないときは$x=1$である。
EがOC上にあるとき$(2<x\leqq4)$は、$OE=x-2$となるので、$(1)(\rm ii)$と同様に考えて
$S=4\cdot\frac12(x-2)(2+2x)$
$=4x^2-4x-8$
$4x^2-4x-8=8$を解いて
$x=\frac{1\pm\sqrt{17}}2$
$2<x\leqq4$より
$x=\frac{1+\sqrt{17}}2$
以上より
$\fbox{$AE=1, \frac{1+\sqrt{17}}2$}$

$(3)$
$AE=x$とすると、$(1), (2)$と同様に考えて、FがOB上にあるとき$(0\leqq{x}<1)$
$S=4\cdot\frac12(2+x)(2-2x)$
$=-4x^2-4x+8$
FがODおよびその延長上にあるとき$(x>1)$
$S=4\cdot\frac12(2+x)(2x-1)$
$=4x^2+6x-4$
⓪
$-4x^2-4x+8=8$を解いて
$x=0, 1$
$0\leqq{x}<1$よりEがAと一致する場合以外には存在しない。
$4x^2+6x-4=8$を解いて
$x=\frac{-3\pm\sqrt{57}}4$
$x>1$より
$x=\frac{-3+\sqrt{57}}4$
以上より、$S=T$となるような点Eの$x$座標は一つある。
①
$-4x^2-4x+8=16$を解いて
$x=-1, 2$
$0\leqq{x}<1$よりこれを満たす$x$は存在しない。
$4x^2+6x-4=16$を解いて
$x=\frac{-3\pm\sqrt{89}}4$
$x>1$より
$x=\frac{-3+\sqrt{89}}4$
以上より、$S=2T$となるような点Eの$x$座標は一つだけある。
②
$x>1$のとき$S=4x^2+6x-4$であるので$S$の最大値は存在しない（無限大に発散する）。
③
FがODおよびその延長上にあるとき$(x>1)$
$OE=2+x, OF=2x-1$である。
$2+x=2x-1$を解いて
$x=3$
このとき$EE’=FF’, EE’\perp{FF’}$となるので、四角形$EFE’F’$は正方形になる。
以上より、$\fbox{①、③}$

$[2]$

$(1)$
余弦定理より
$t^2=8^2+x^2-2\cdot8\cdot{x}\cos60^\circ$
$\fbox{$x^2-8x+64-t^2=0$}$

$(2)$
$x>0$より、これが異なる二つの正の解をもつような$t$の値の範囲を求める。
よって解答は$\fbox①$

$(3)$

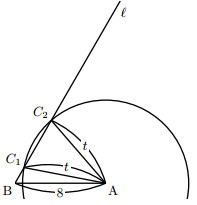
上図より、点Aを中心とし、半径$t$の円が$\ell$と異なる2点で交わるような$t$の値の範囲を求める。
よって解答は$\fbox{⓪}$

$(4)$
$(1)$と同様に、$BC=x$とおくと、余弦定理より
$b^2=a^2+x^2-2ax\cos\theta$
$x^2-2a\cos\theta{x}+a^2-b^2=0\cdots\ast$
$\ast$の判別式をDとする。
また、$f(x)=x^2-2a\cos\theta{x}+a^2-b^2$とする。
$f(x)$は下に凸の2次関数であり、軸は$a\cos\theta$である。
$\theta$は鋭角なので$\cos\theta>0$であり、また$a>0$であるので、軸は正である。
$(ア)$　$\ast$が異なる二つの正の解をもつような$a, b, \theta$の関係を求める。

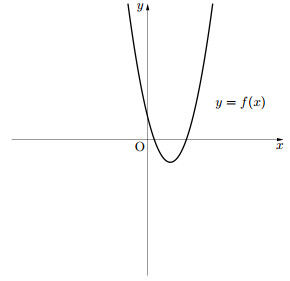
このとき、図より、$D>0$かつ$f(0)>0$である。
$\frac{D}4=a^2\cos^2\theta-a^2+b^2>0$
$a^2(\cos^2\theta-1)+b^2>0$
$b^2>a^2(1-\cos^2\theta)$
$b^2>a^2\sin^2\theta$
$b>0, a\sin\theta>0$より
$b>a\sin\theta$
$f(0)=a^2-b^2>0$
$a^2>b^2$
$a>0, b>0$より
$a>b$
以上より、$a\sin\theta<b<a$
$(イ)$　$\ast$が一つだけ正の解をもつような$a, b, \theta$の関係を求める。
$(A)$　$\ast$が正の解と負または0の解を一つずつもつ

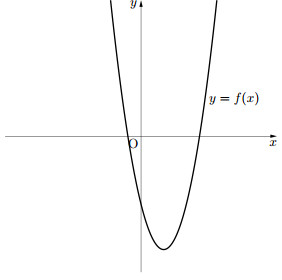
このとき、図より、$f(0)\leqq0$
$(ア)$と同様に考えて
$a\leqq{b}$
$(B)$　$\ast$が正の重解をもつ

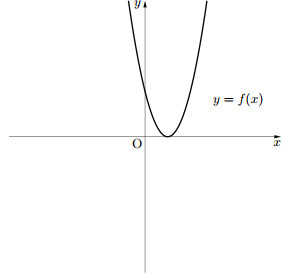
このとき、図より、$D=0$
$(ア)$と同様に考えて
$b=a\sin\theta$
$(ウ)$　$\ast$が一つも正の解をもたないような$a, b, \theta$の関係を求める。

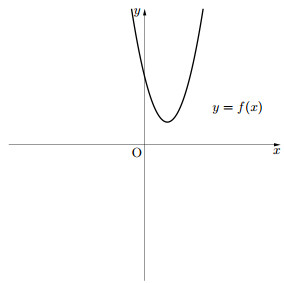
このとき、図より、$D<0$
$(ア)$と同様に考えて
$b<a\sin\theta$
以上の議論はそれぞれその逆も成り立つので

モデル問題例4
$[1]$

$(1)$
求める角を$\theta$とする。

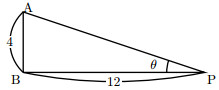
図より、$\tan\theta=\frac{4}{12}=0.333\cdots$
三角比の表より$\tan\theta=0.333\cdots$となる$\theta$は$18^\circ$と$19^\circ$の間なので
解答は$\fbox{⑦}$

$(2)$
$(\rm i)$
$\cos\angle{APB}>0$であれば$\angle{APB}$は鋭角で、
$\cos\angle{APB}=0$であれば$\angle{APB}$は直角で、
$\cos\angle{APB}<0$であれば$\angle{APB}$は鈍角である。
余弦定理より
$AB^2=AP^2+BP^2-2\cdot{AP}\cdot{BP}\cdot\cos\angle{APB}$
$2\cdot{AP}\cdot{BP}\cdot\cos\angle{APB}=AP^2+BP^2-AB^2$
$\cos\angle{APB}=\frac{AP^2+BP^2-AB^2}{2\cdot{AP}\cdot{BP}}$
よって、$\fbox{$\frac{AP^2+BP^2-AB^2}{2\cdot{AP}\cdot{BP}}$が0より大きければ$\angle{APB}$が鋭角であることを確かめることができる。}$

$(\rm ii)$
その関係式は、正弦定理より
$\fbox{$\frac{AB}{\sin\angle{APB}}=2R$}$
$\sin\angle{APB}=\frac{AB}{2R}$
$AB$が一定のとき、$R$が小さくなればなるほど$\sin\angle{APB}$は大きくなる。そして$\angle{APB}$が鋭角のとき、$\sin\angle{APB}$が大きくなればなるほど、$\angle{APB}$が大きくなる。

$(\rm iii)$
①
台座の地面から$1.5m$の点をH、ABの中点をC、見込む角を$\theta$とする。

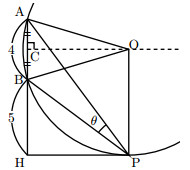
図より、$R=OP=CH=2+5=\fbox{7}$
②
$(\rm ii)$で述べたように、正弦定理より
$\frac{4}{\sin\theta}=14$
$\sin\theta=\frac27\fallingdotseq0.286$
三角比の表より、$\sin\theta=0.286$となる$\theta$は$16^\circ$と$17^\circ$の間なので
解答は$\fbox{③}$
③
$\bigtriangleup{AOC}$において三平方の定理より
$7^2=2^2+CO^2$
$CO^2=45$
$CO>0$より
$CO=3\sqrt5\fallingdotseq6.71$
銅像の真下と「ベストスポット」の距離HPはCOに等しいのでおよそ6.71$m$である。
よって解答は$\fbox{③}$

以上です。2次関数や三角比を習った人なら理解できるように書いたつもりですので、独習などにご活用ください。