はじめに
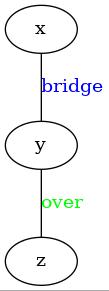
バルーンアートで数学の正多面体を作っています。作成方法は複数あるのですが、今回は静岡大学の藤間信久教授による技法を紹介します(以下藤間法と呼ぶ)。藤間法では、すべての節点をピンチツイストで表現し、それらによる複数のバブルを束ねて正多面体の頂点とします。藤間法の詳細は参考資料[1][2]を見て下さい。[1]は藤間教授にメールすれば貰えます。参考資料[3][4]ではピンチツイストを含む基礎技法が紹介されています。藤間教授には講座資料を頂くだけでなく、質疑応答、組立手順の助言を頂くなど大変お世話になりました。有難うございます。
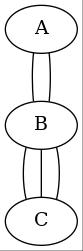
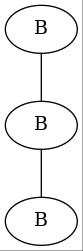
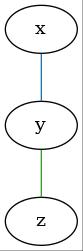
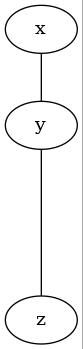
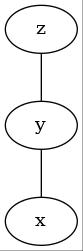
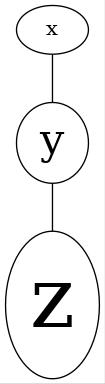
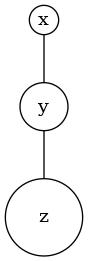
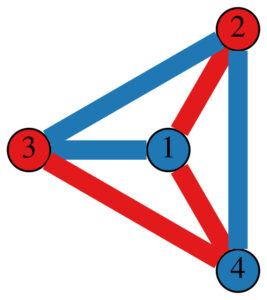
現状では正多面体の内4種類、正4面体、正6面体、正8面体、正12面体を組立てることができました。残る正20面体は、私のスキルでは組立不可能でした。出来た事と出来なかった事を合わせて解説します。以下では正多面体の設計図と完成写真を示します。設計図の丸Pはピンチツイスト(Pinch Twist)によるバブルを表します。
正4面体
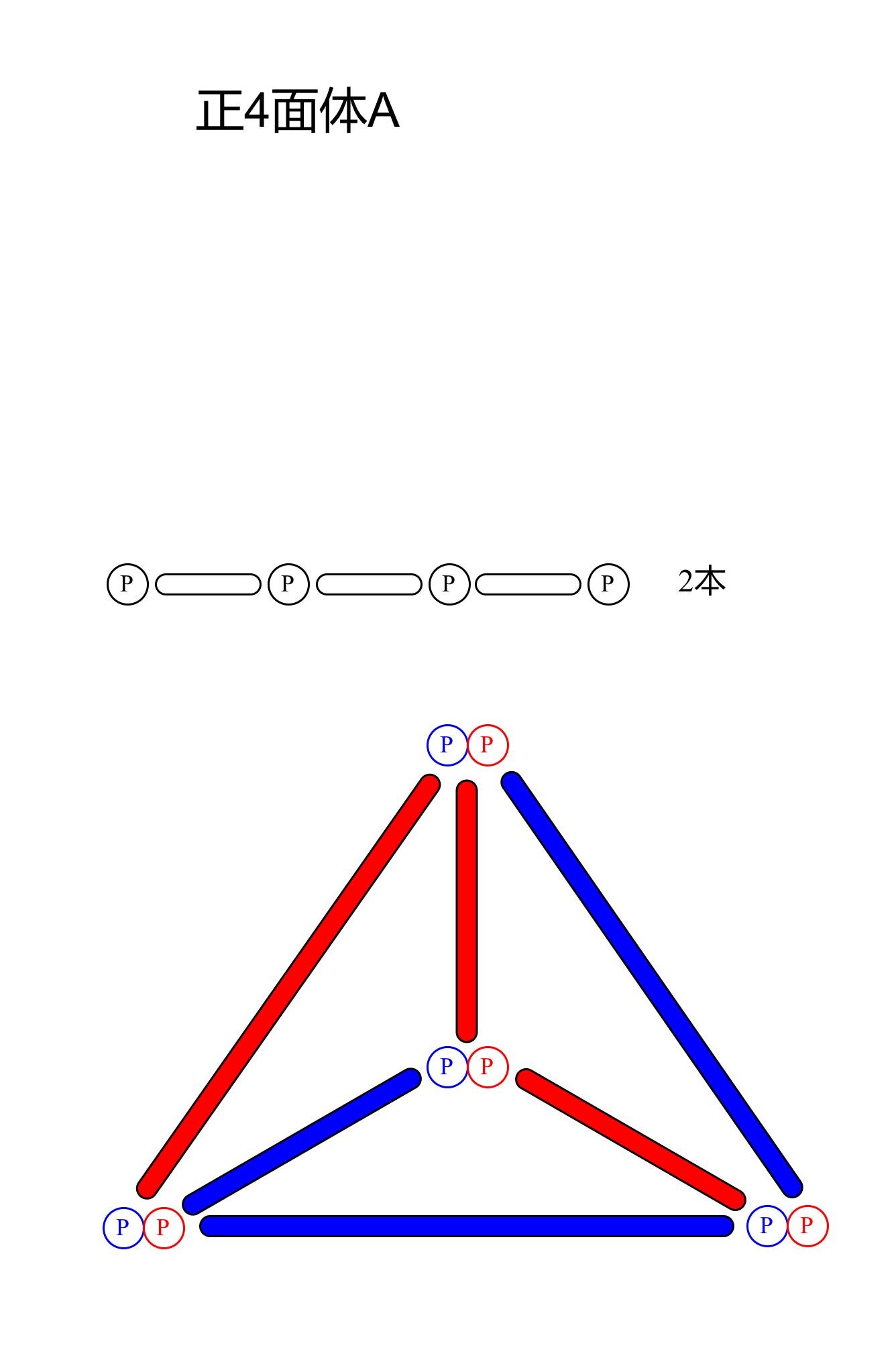
正4面体A

正4面体A
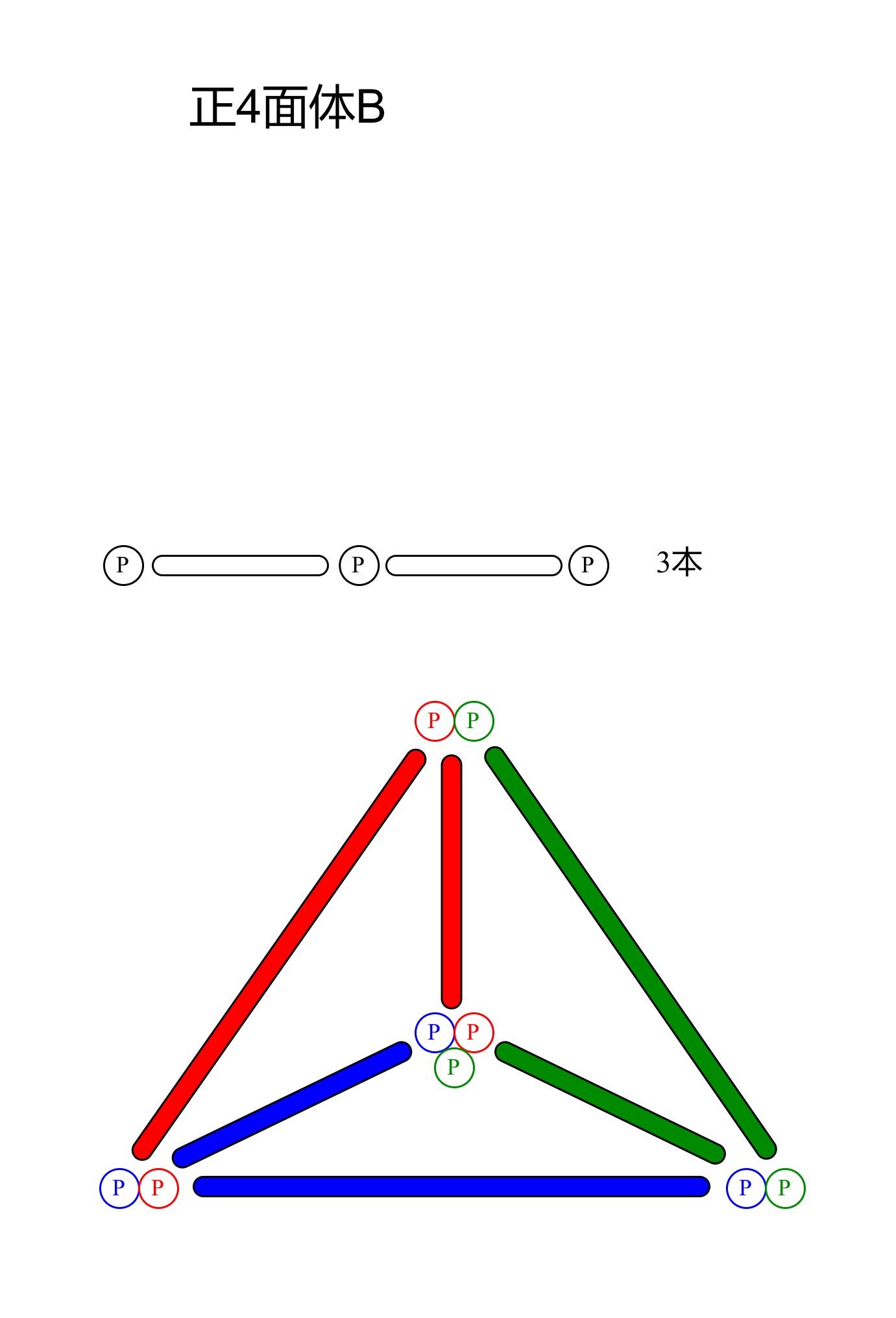
正4面体B

正4面体B
正6面体
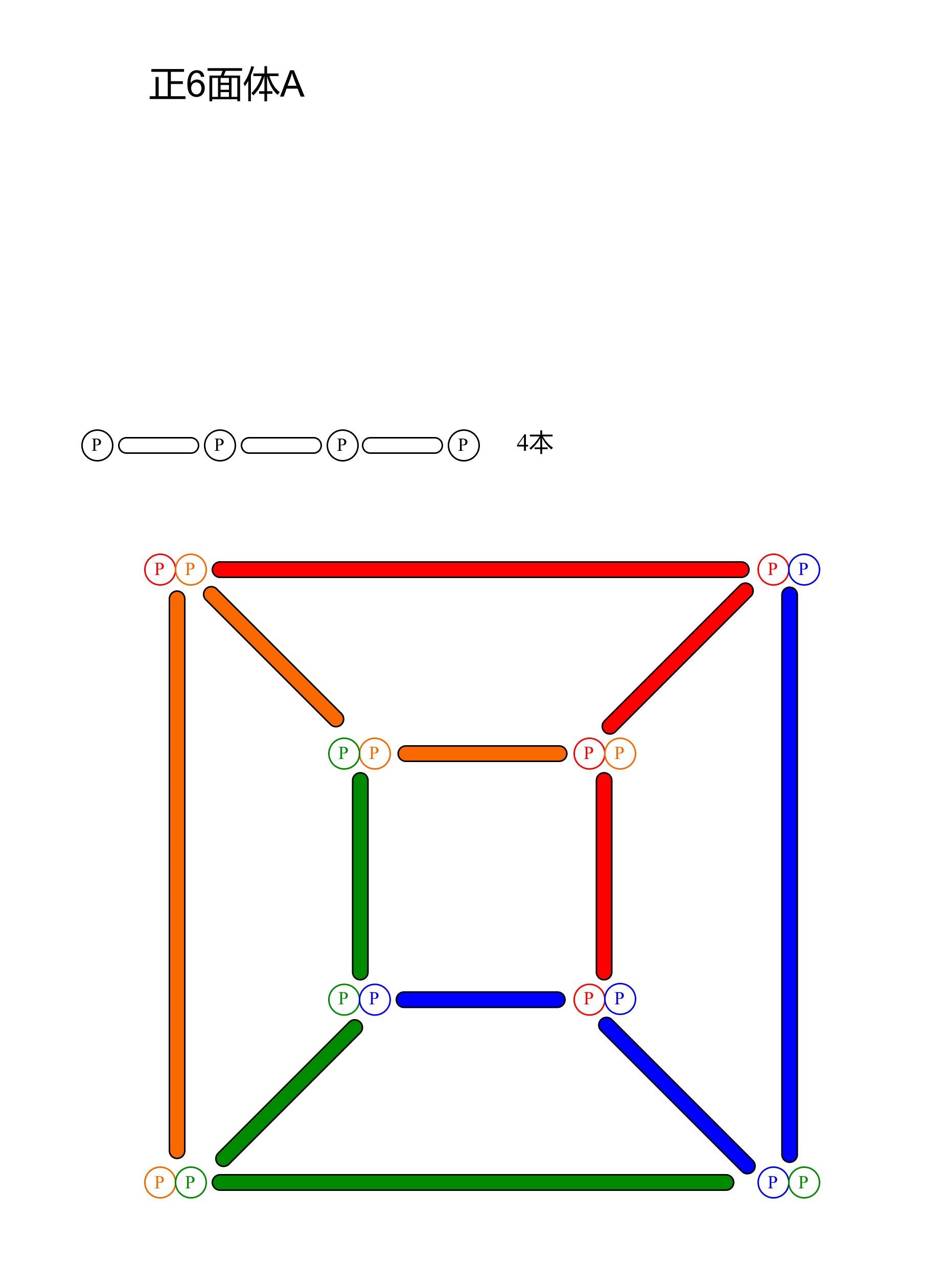
正6面体A

正6面体A
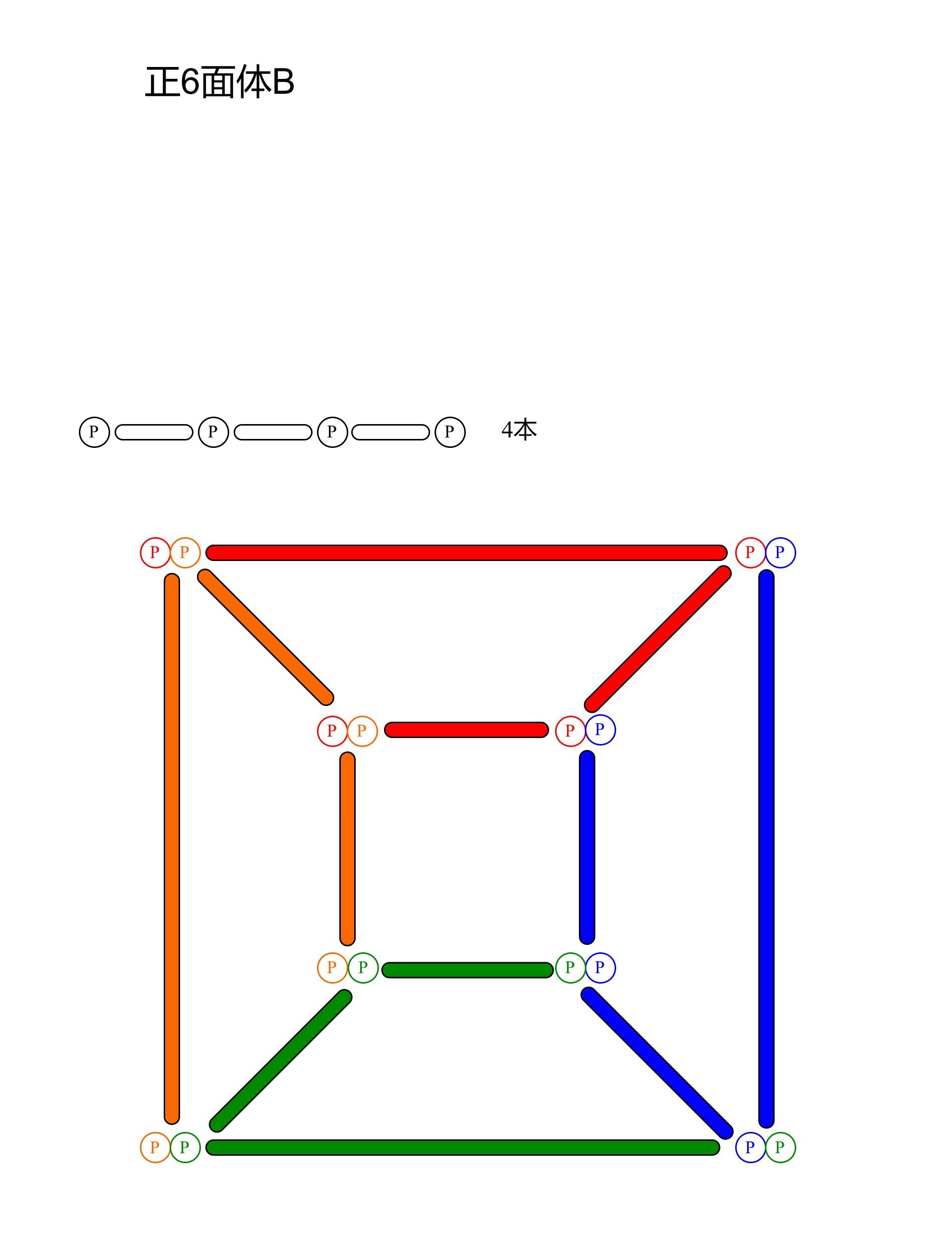
正6面体B

正6面体B
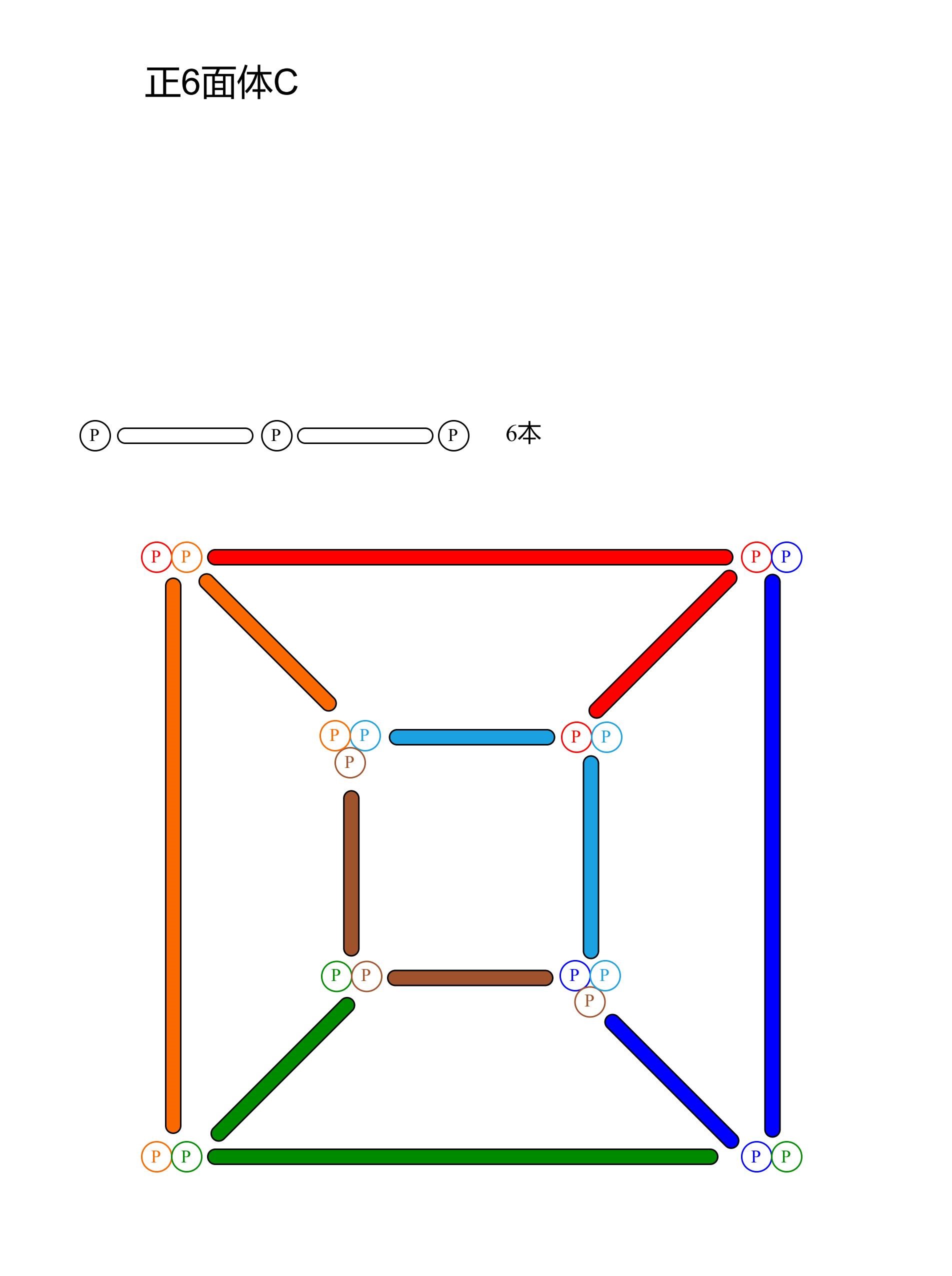
正6面体C

正6面体C
正8面体
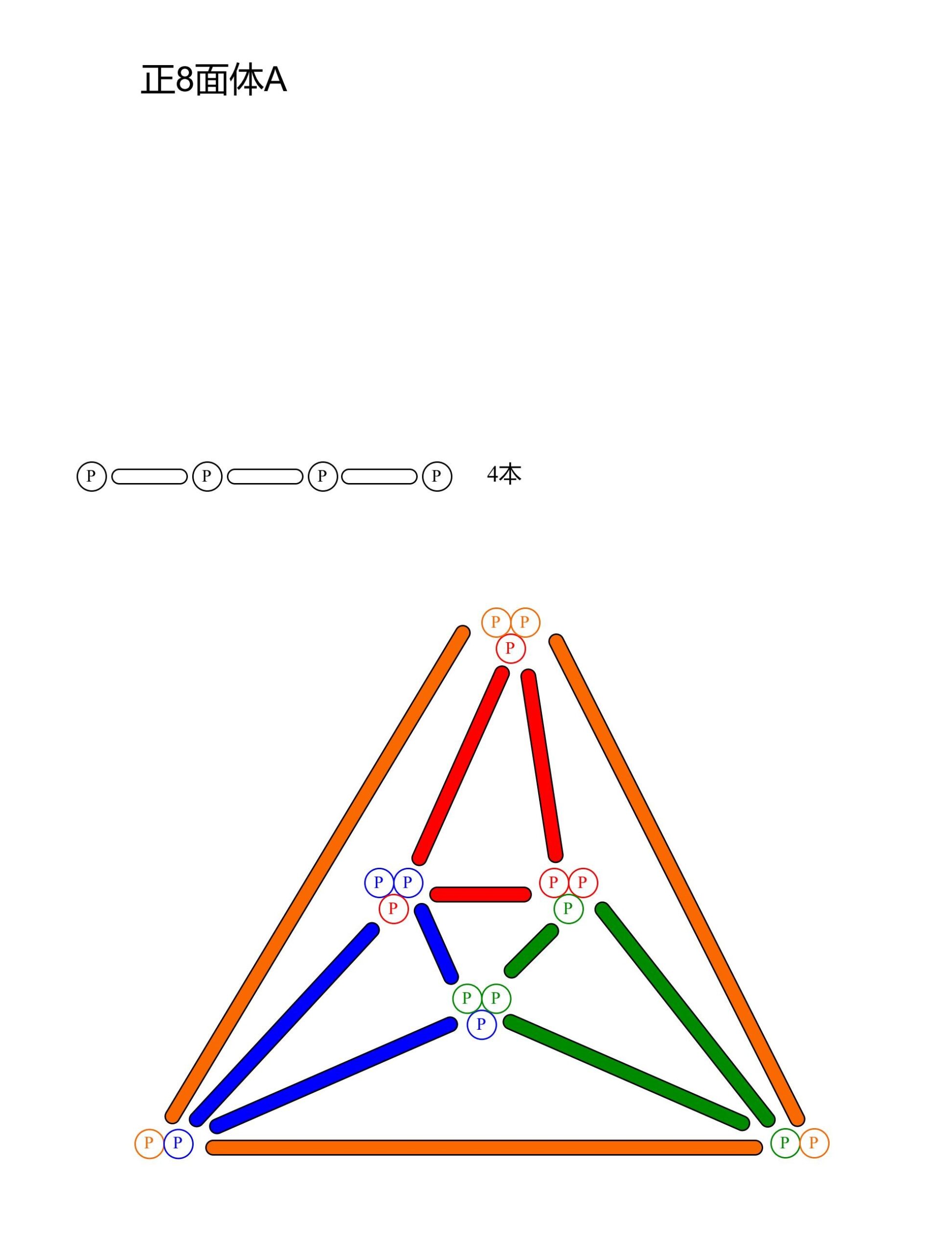
正8面体A

正8面体A
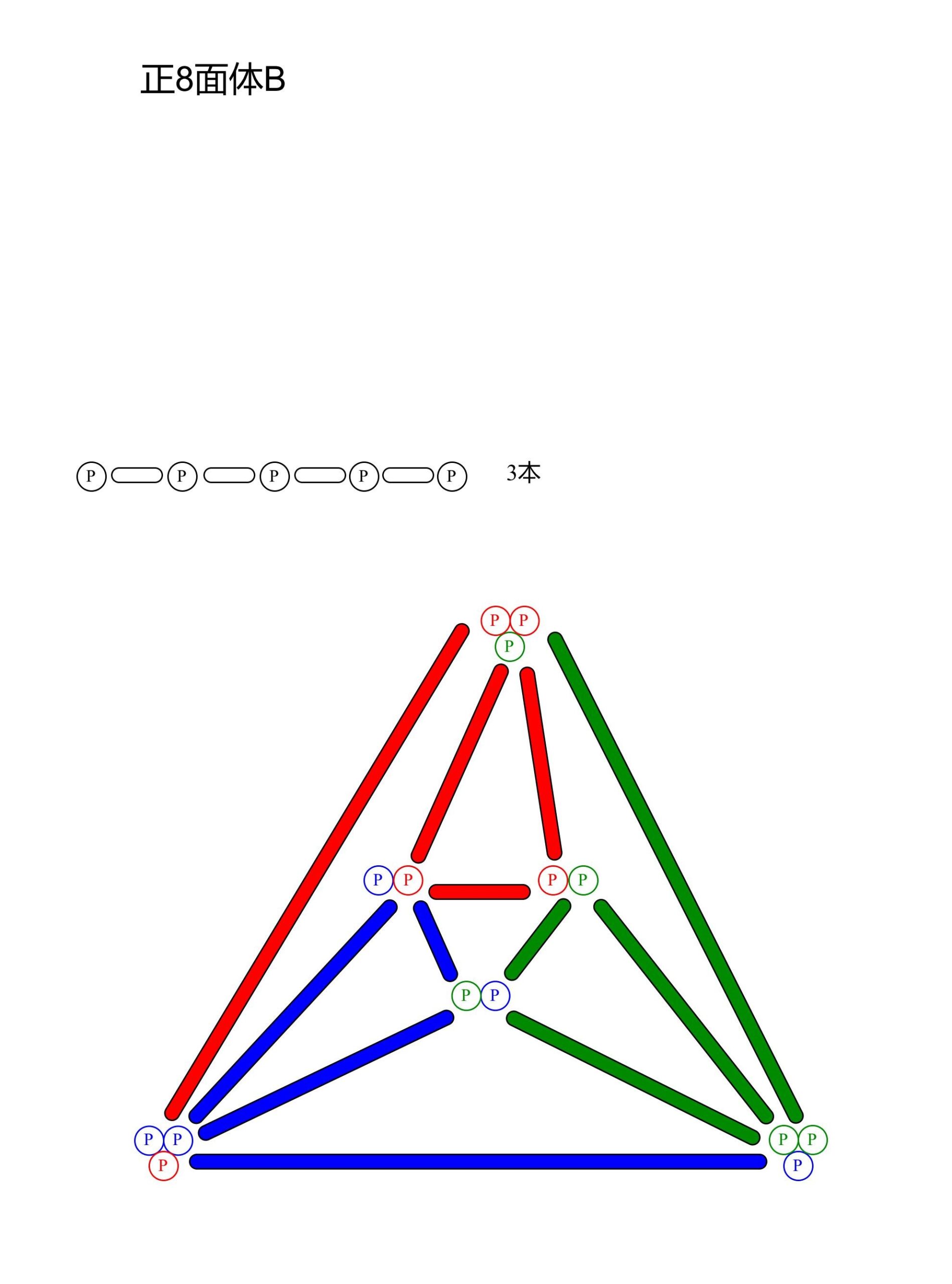
正8面体B

正8面体B
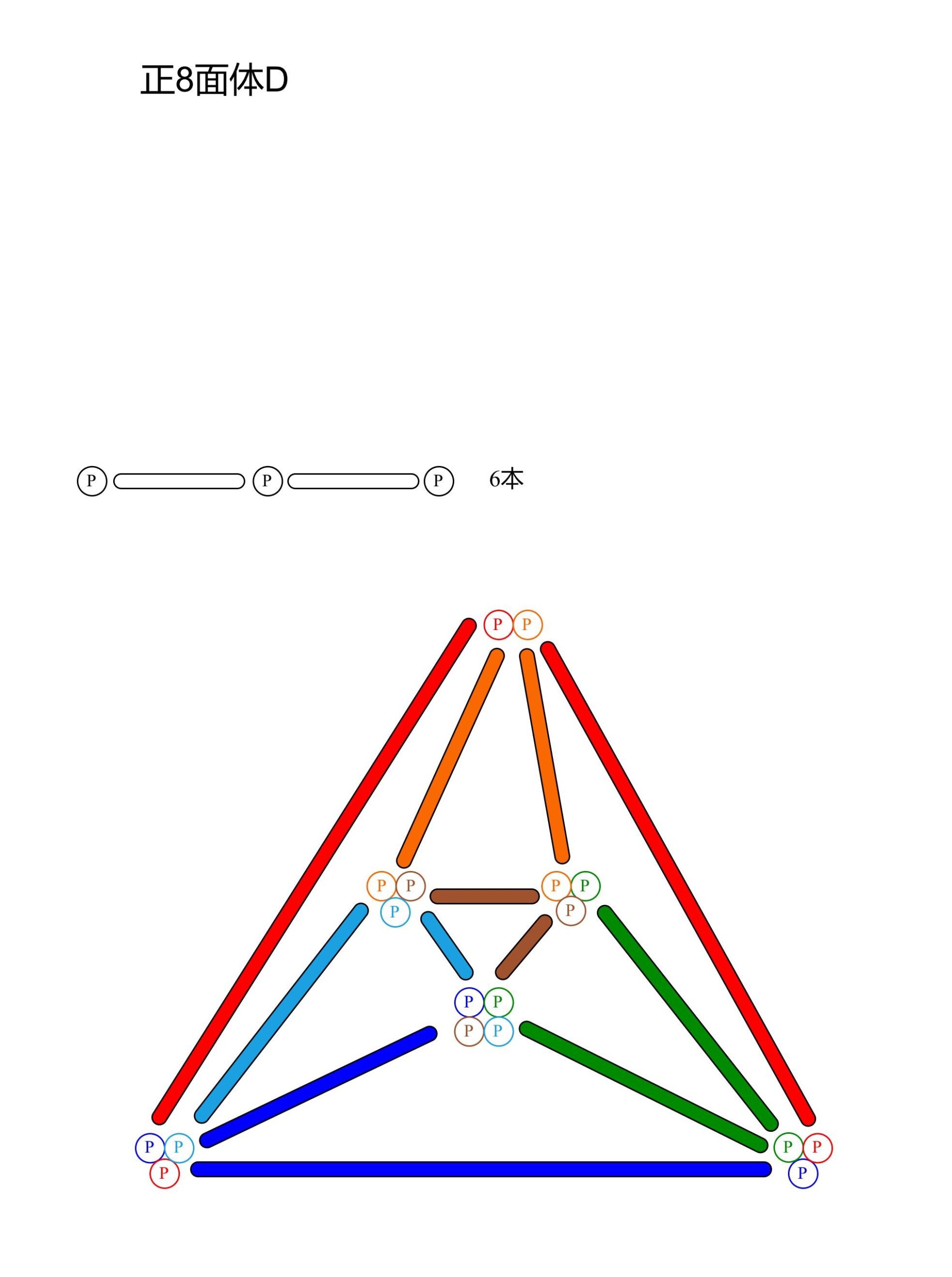
正8面体D

正8面体D
正12面体
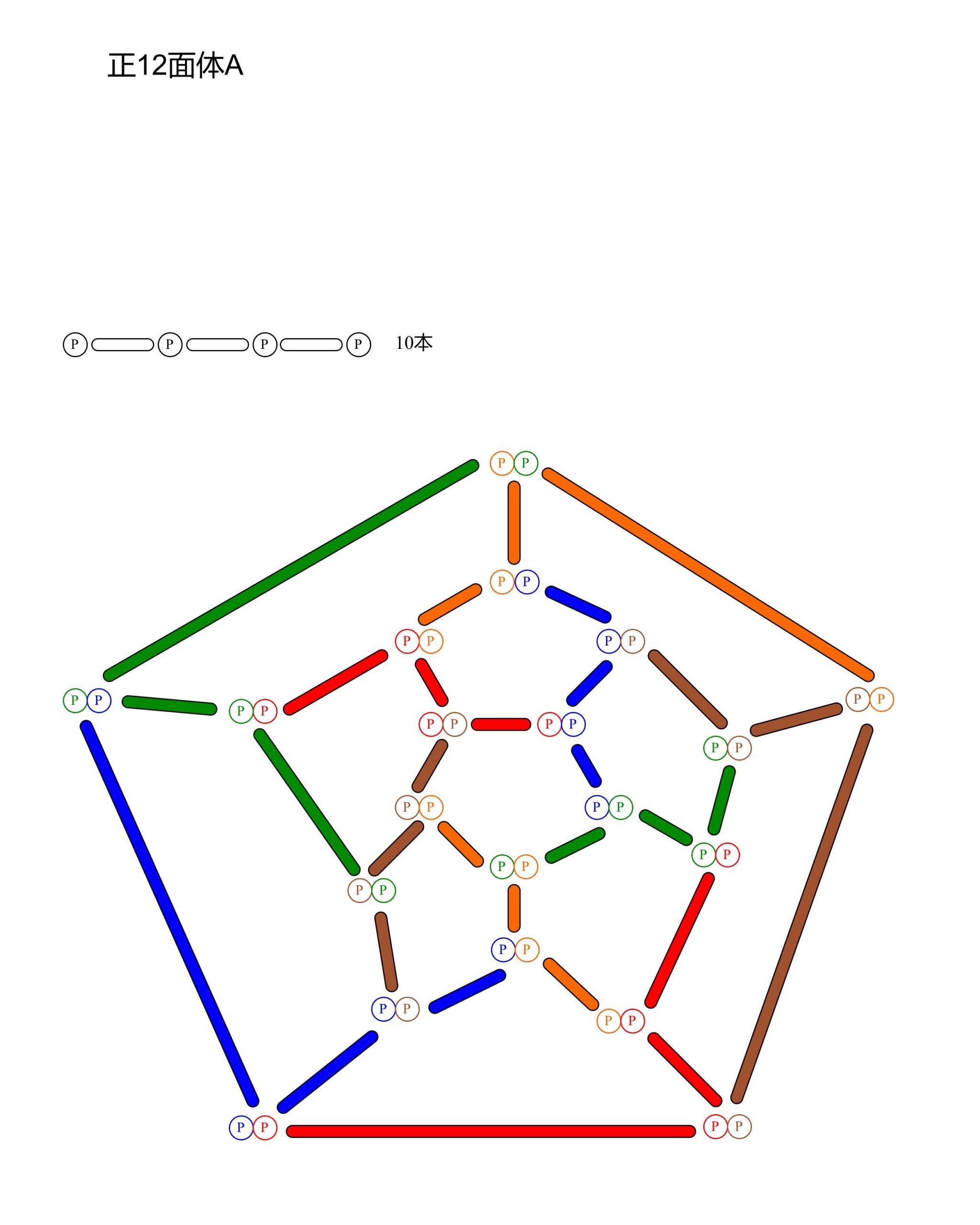
正12面体A

正12面体A
正20面体
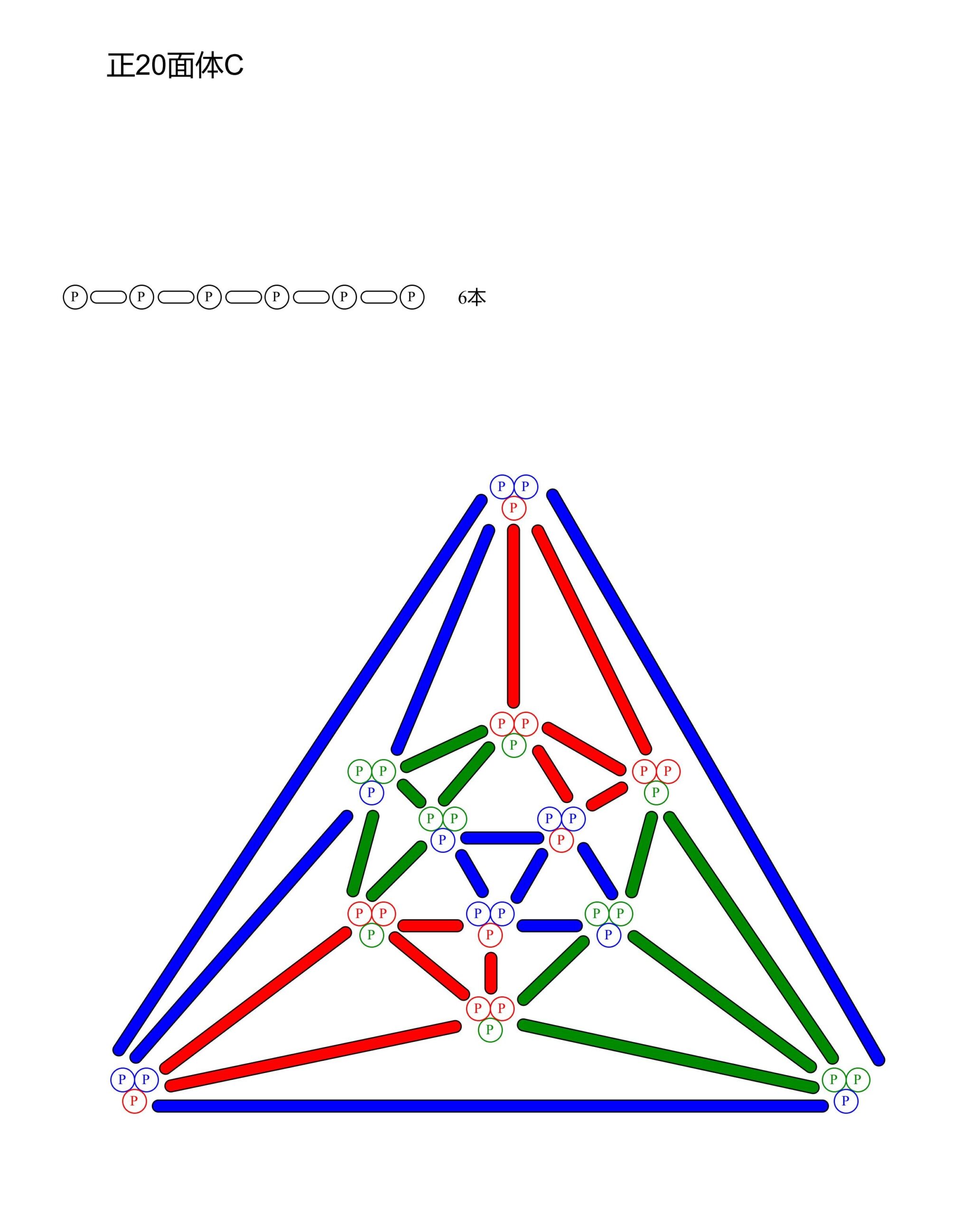
正20面体C
正20面体Cは組立不可能でした。1本のバルーンに6個のピンチツイストこぶを作ると、1辺の長さが8センチぐらいになりました。これでは短すぎて組立てられません。
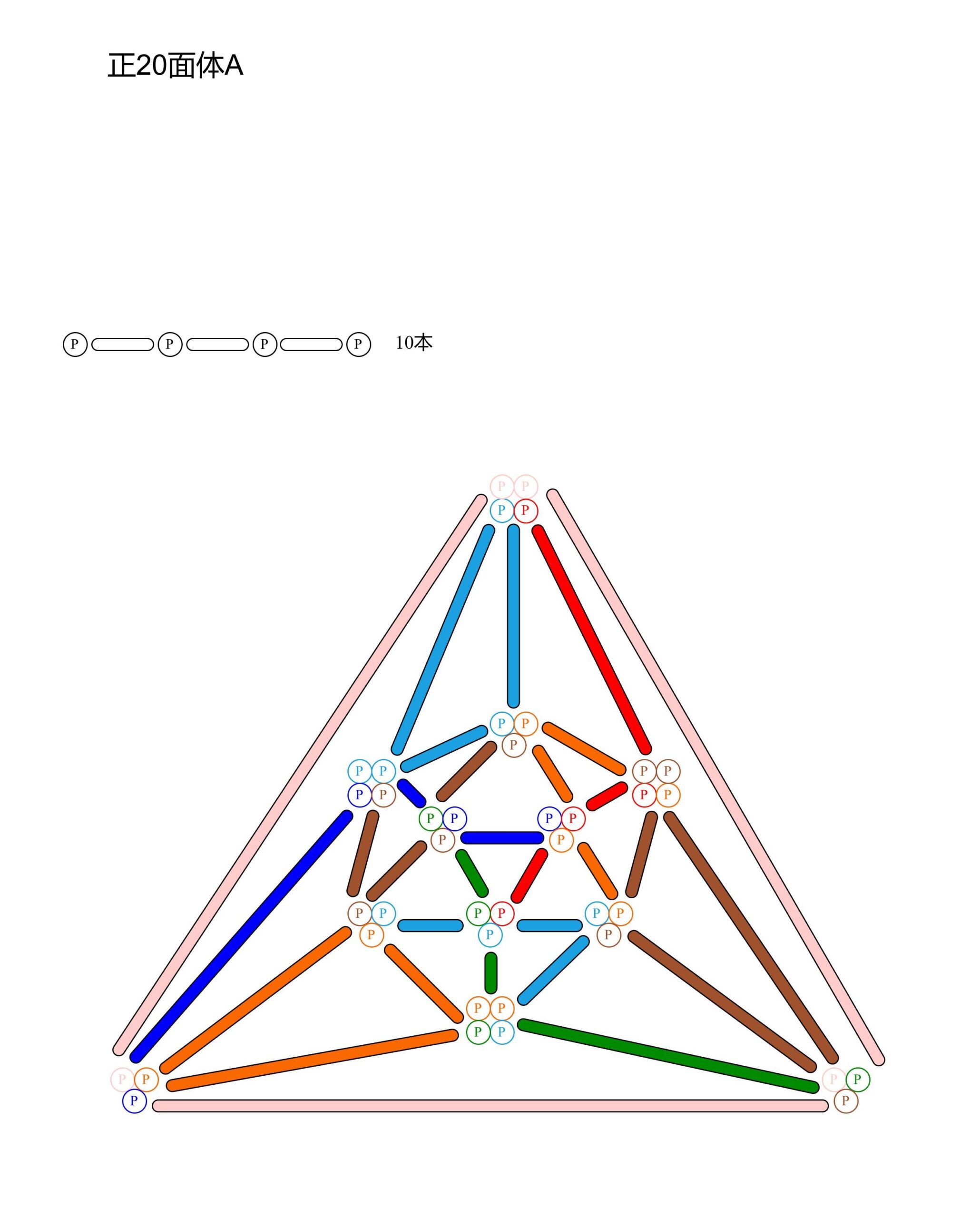
正20面体A
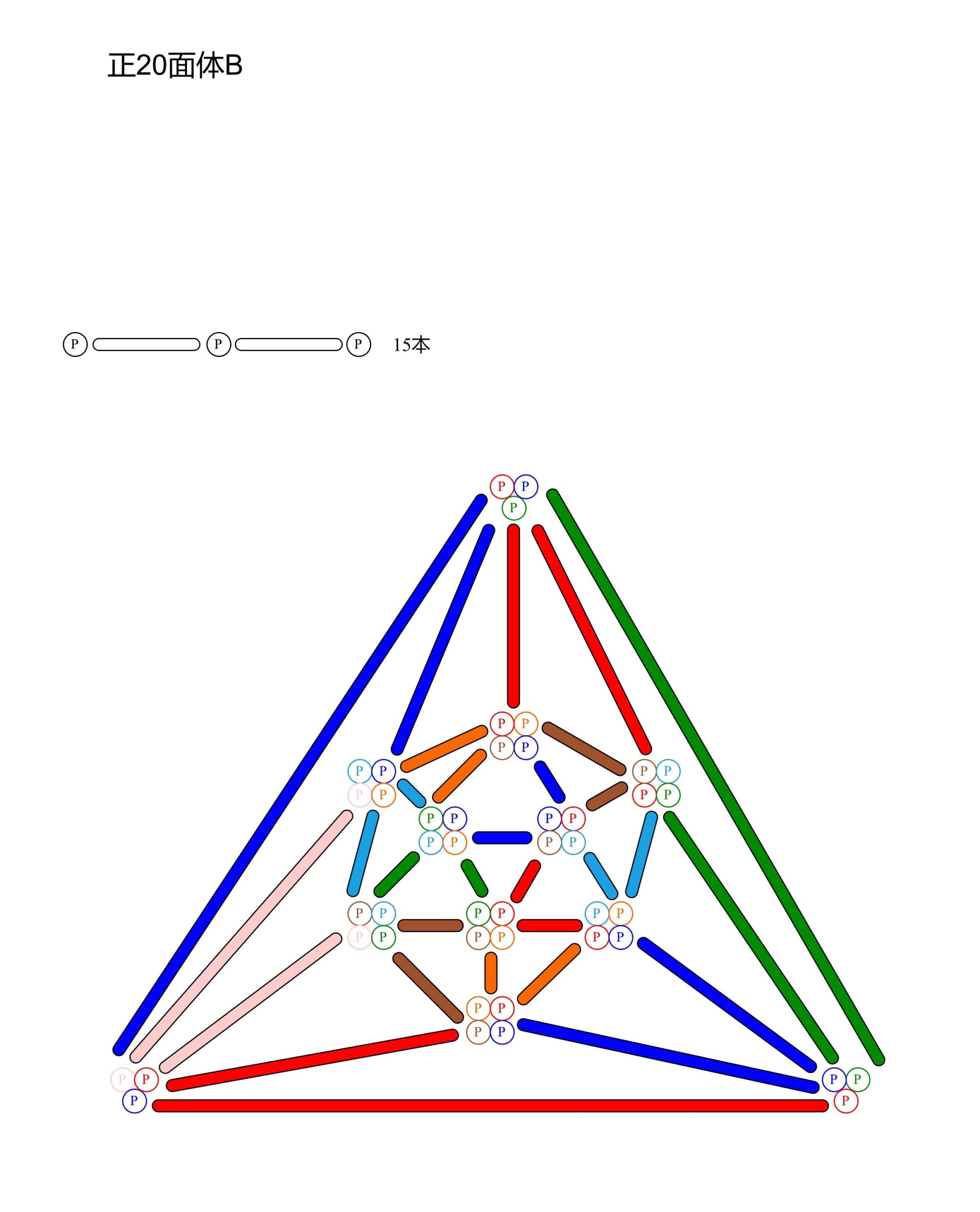
正20面体B
正20面体ABは組立不可能でした。バルーン同士が絡み合って丸い形になってくれません。何が悪いのかいまいち分かりませんでした。設計も組立手順も悪くないと思うのですが、、、。正20面体は今後の課題とします。

正20面体Aが絡まっている状態
参考資料
[1] 藤間信久, 2017, バルーンアートで学ぶ 正多面体の幾何学
これは公開講座の講義資料で、藤間教授にメールすると頂けます。
藤間教授の連絡先は、https://train1.eng.shizuoka.ac.jp/fujima/collaborator.htmlに記載。
[2] 鈴木伊織, 2017, バルーンアートで学ぶ『正多面体の幾何学』, トップガンジャーナル 第26号, https://topgun.ed.shizuoka.ac.jp/topgun-journal/
藤間教授が開催した公開講座の様子が報告されています。
[3] Masayoshi Matsumoto, 2023, バルーンアートのはじめ方 ~これだけで大体 OK!基礎技法集~ Ver1.24. , https://isopresso-shop.booth.pm/items/847287
無料のPDFファイルがダウンロードできます。
[4] Masayoshi Matsumoto, 2020, バルーンアートの基礎技法 10 選 / 10 Basic Skills to Make Balloon Animals, https://www.youtube.com/watch?v=xFI6UjOjR7o
上記の基礎技法集に対応した動画です。
[5] 藤原大樹, 2025, 設計図(藤間法)
[6] 藤原大樹, 2025, 組立手順書(藤間法)
作成: 藤原大樹
更新: 2025年1月15日