昔の人々がどのように地球の大きさを測定したかをまとめました。影を用いた測定法、星を用いた測定法、山を用いた測定法の3つがあります。
PDFファイル
作成: 藤原大樹
更新: 2023年3月6日
昔の人々がどのように地球の大きさを測定したかをまとめました。影を用いた測定法、星を用いた測定法、山を用いた測定法の3つがあります。
PDFファイル
作成: 藤原大樹
更新: 2023年3月6日
フリーランスの知人に依頼して、英語の音声教材を作成してもらいました。利点や今後の課題が見えてきたので、そのことについて執筆します。
私は趣味で英語の勉強をしています。塾に通っているわけではなく、完全に独学でやっています。最近は英単語力強化、いわゆるVocabulary Buildingに力を入れています。使用している英単語帳は「一杉武史著 改訂版 キクタン英検1級 アルク社」です。どうやって勉強するかというと、英単語帳の短いフレーズを何度も音読します。大学受験用のシステム英単語と同じ勉強方式です。さらに、リスニング力を向上させるには、自分で発音するだけでなく、音声教材のお手本を聴くことが重要です。ところが、キクタンでは長い例文の音声ファイルはありますが、短いフレーズには音声ファイルがありません。困ったことにリスニングの練習ができません。1つの解決策はネイティブスピーカーに依頼して音声教材を作成してもらうです。しかし、この方法はお金がかかり過ぎて無理です。2つ目の解決策は、人工知能を活用して音声教材を作るです。これは比較的安くできるのではないかと閃きました。
実はQuizletという無料のWebアプリがあります。Quizletは自作の単語カードを作って、Web上で暗記していくというシステムです。Quizletは単語カードを人工知能による音声で読み上げてくれます。しかし、英語の読み上げは少し不自然です。Quizletより自然な英語音声で勉強したいと思いました。
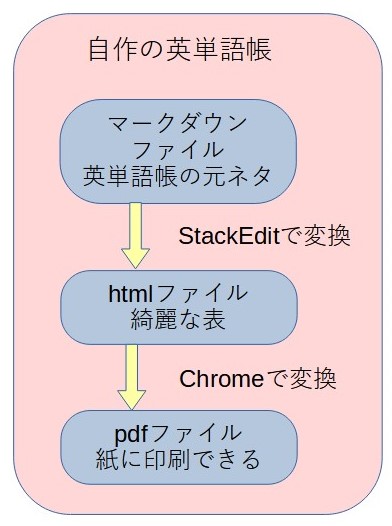
人工知能に英語を喋ってもらうためには、まず自作の英単語帳を作成する必要があります。今回はマークダウンファイルの表を用いて英単語帳を作ります。表の各行はフレーズを表します。そして表の各列は、ID番号、英語フレーズ、日本語フレーズ、コメントの4つです。マークダウンの実体はただのテキストファイルです。しかし、マークダウンは手軽に綺麗なドキュメントに変換できます。マークダウンファイルをhtmlファイルに変換することで綺麗な表ができます。その変換をするのはStackEditという無料のWebアプリです。次に、htmlファイルをPDFファイルに変換すれば、印刷できる状態になります。その変換をするのはChromeという無料のブラウザです。


今回音声教材を作成するにあたって、Google社のWaveNetという人工知能を活用します。WaveNetはText-to-Speechという種類のソフトウェアで、文字情報を音声情報に変換してくれます。簡単にいうと原稿を読み上げるアナウンサーの役割を果たす人工知能です。高性能な人工知能なのですが、下記のサイトに無料の試用デモがあります。とりあえず、試用デモを動かして自分の好きな言葉をWaveNetに喋らせて下さい。音声が自然で人間に近いことが分かると思います。
https://cloud.google.com/text-to-speech
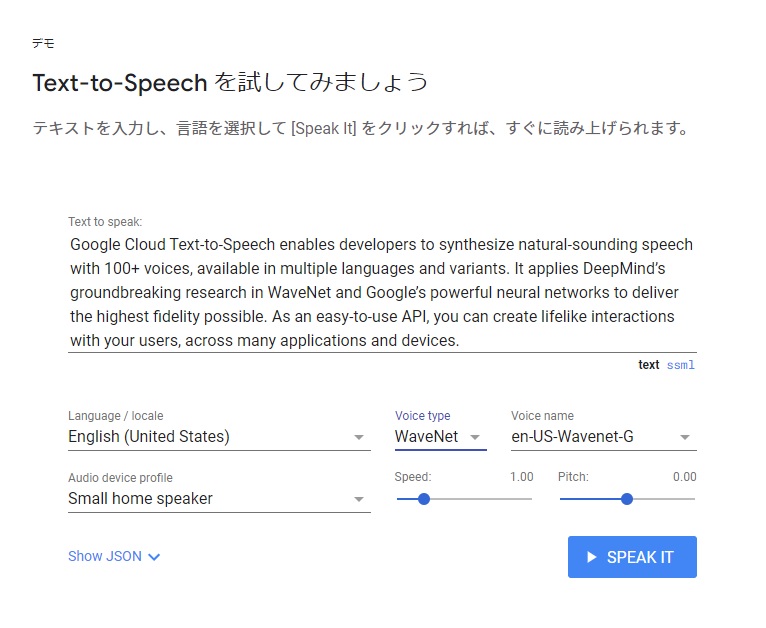
WaveNetは英語と日本語だけでなく、40以上の言語を喋ってくれます。そして、男女の声質が準備されています。利用料金は有料ですが、100万文字あたり$16米ドルで格安です。更に、最初の100万文字は毎月無料です。なので、英単語帳一冊分を読み上げるだけなら、実質無料で毎月利用できます。ただし、クレジットカード情報をGoogleに登録する必要があります。
必要な技術はプログラミング言語Pythonの入門レベルだけです。一般に、人工知能を活用するには高度な専門的知識が必要になります。しかし今回は、専門的知識は全く必要ありません。その理由は、WaveNetとPydubが直感的なPythonのAPIを提供してくれるからです。難しくはないが、時間と手間が掛かるという認識です。
Pythonプログラムを活用するに当たって、パソコン環境を整備する必要があります。以下の手順で行います。
Step1. 人工知能WaveNetを使える様にパソコン環境を整備する。
下記のYoutube動画を参考にします。
下記のPythonプログラムも参考になります。
https://gist.github.com/coding-youtuber/e8a2970bde14e08b5854fab5ae8003e4
Step2. PythonのライブラリPydubをインストールする。
Pydubは直感的なAPIで音声ファイルを連結できます。音声の連結は足算記号+で実現できます。
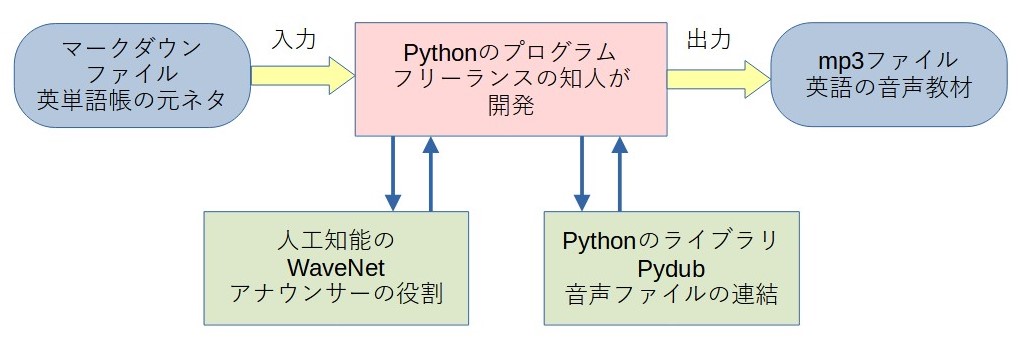
Pythonのプログラムを用いて音声教材を作成します。入力は英単語帳であるマークダウンファイルです。出力は音声教材であるmp3ファイルです。次の手順でPythonプログラムは動作します。
Step1.英語音声と日本語音声のそれぞれを作成する。
Step1.1 英語音声をWaveNetで作成する。
英語フレーズをアメリカ英語、Speed=0.85でmp3ファイルを作成する。
Speed=1.00は英語ネイティブの標準スピードなので速すぎます。Speed=0.85にすると少しゆっくり目で丁度良いです。
Step1.2 日本語音声をWaveNetで作成する。
日本語フレーズをSpeed=1.00でmp3ファイルを作成する。
日本語は標準スピードで問題ありません。
Step2. 英語音声と日本語音声を連結する。
Pydubを用いて英語と日本語のファイルを連結する。
1フレーズに対して、「英語から日本語へ」と「日本語から英語へ」の2種類のmp3ファイルを作成する。音声ファイルを連結する際に、下記の様に空白音声を入れる。
(英日ファイル) = (英語フレーズ) + (2秒間の空白) + (日本語フレーズ) + (2秒間の空白)。
(日英ファイル) = (日本語フレーズ) + (2秒間の空白) + (英語フレーズ) + (2秒間の空白)。
ファイル名は「ID番号.mp3」とする。
コメント列及びID番号列は読み上げない。
WaveNetは非常に賢い人工知能ですが、たまに漢字を誤読します。例を二つ挙げると、
例1:入力「口げんかはもう止(や)めなさい!」
=> WaveNet「口げんかはもう止(ど)めなさい!」
例2:入力「あなたの家までお供(とも)する」
=> WaveNet「あなたの家までお供(きょう)する」
などがあります。訓読みすべき漢字を音読みしてしまうという傾向があります。この問題は、入力をひらがなやカタカナにすることで取り敢えずは解決できます。例1だと、入力を「口げんかはもうやめなさい!」にするだけです。
実務上は次の手順で音声教材を改定します。
Step1. 音声ファイルを自分の耳で聴いて精密検査する。
Step2. 修正箇所の一覧表をマークダウン形式で作成する。
Step3. 修正箇所一覧表をPythonプログラムへ入力し、誤読のない音声ファイルを作成する。
Step4. 修正した音声ファイルで古い音声ファイルを上書きする。
Step5. 音声教材全体の最終検査をする。

さっそく音声教材を用いて英語のトレーニングをしてみました。リスニング力を向上させられそうな予感がしました。ほぼほぼ満足しています。日本語音声は少しだけ不自然です。将来的にGoogle社にWaveNetを改善してもらうしかないです。しかし不思議なもので不自然な音声でも数回聴くうちに耳が慣れます。日本語音声の不自然さは、仕方ないと諦めます。一方英語音声は、ネイティブ発音に完璧に近いと言える水準なので、大満足です。ただ、英語音声の方でも、少し怪しい発音を発見しました。例を挙げます。
“at the zenith of his career”と聴こえたでしょうか? 残念ながら私の耳にはそうは聴こえなかったです。聞き取り不可能でした。この現象は、私の英語耳が悪いのか、WaveNetが悪いのかは判断できません。したがって、英語音声についてもこれ以上の追求は行いません。
実は数年前に今回と同じように人工知能を用いて音声教材を作成しようとしました。その当時の合成音声技術は現在と比べてとても低かったです。非ネイティブの私が聴いても、英語音声は明らかに不自然でした。この数年間で技術の進歩があり、今回はGoogle社のWaveNetを利用することで、英語学習の実用に耐えうる音声教材を作成できました。
作成: 藤原大樹
更新: 2022年12月24日
京都アカデメイアの泊昌史正会員が、静岡県舞台芸術センターの劇評コンクールで最優秀賞を受賞しました!
劇評本文は以下のリンクから読めます。演劇にご関心のある方は是非ご覧になってみてください。
公式
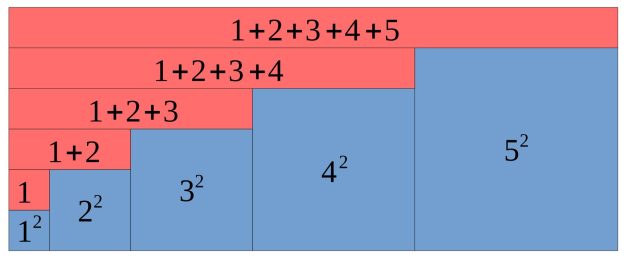
\[
1^2+2^2+3^2+ \dots + n^2 = \frac{1}{6}n(n+1)(2n+1)
\]
を4通りの方法で証明しました。
高校数学は奥が深いです。
そして更に、公式
\[
1^3+2^3+3^3+ \dots + n^3 = \frac{1}{4}n^2(n+1)^2
\]
を3通りの方法で証明しました。
作成: 藤原大樹
更新: 2022年8月17日

高校数学を復習しています。
公式
\[
1+2+3+ \dots + n = \frac{1}{2}n(n+1)
\]
を3通りの方法で証明しました。
作成: 藤原大樹
更新: 2022年8月9日
抜群に面白い入試問題を見つけたので、紹介します。ネイピア数$e$が無理数であること及び$e = \sum_{k=0}^\infty \frac{1}{k!}$であることの2つを証明します。入試問題なので高校数学しか使いませんし、問題の難易度はセンター試験レベルです。模範解答と問題解説をPDFファイルにまとめました。よかったら見て下さい。
作成: 藤原大樹
更新: 2022年8月6日
正会員の舟木です。昨日で終了した中江兆民『三酔人経綸問答』につづき、京アカ輪読会では別の本にとりかかる予定です(早くて再来週の水曜スタート)。
次に読む本の候補を昨日ご参加のみなさんに挙げてもらいました。そのなかから、長すぎず、入手しやすそうなものをピックアップしました(ほぼ作者五十音順)。複数回答歓迎(五冊まで)ですので、「①と③と⑤がいい!」みたいな形で希望の番号をkyotoacademeia@gmail.comまでご連絡ください。すでに何人かからお返事いただいています。何日か待ってみて、票数の多いものを次の本として選びます。
もちろん、リクエストした本に決まったからと言って毎回参加しないといけない、なんてことはないです。いろいろ忙しいのはみなお互い様ですので、どなたでも、ご無理のないペースでご参加ください。
①新井白石『折りたく柴の記』:江戸の才人新井白石の自伝。中江兆民の「三酔人」と同じく桑原武夫による現代語訳あり。
②岡倉天心『茶の本』:本輪読会で以前に扱った新渡戸稲造・内村鑑三と同世代の文化人。茶道の聖書。訳本いろいろ。英文つきなら講談社学術文庫。
③河上肇『貧乏物語』:戦前の代表的経済学者が貧困の発生構造を解明した名著。岩波文庫のほか、佐藤優が解説した講談社現代新書版もあり。
④E.H.カー『歴史とは何か』:歴史家カーの名講演。清水幾太郎訳の岩波新書のほか、最近は新訳も出た模様。
⑤九鬼周造『いきの構造』:「いき」と「やぼ」のいき。日本哲学の古典。岩波文庫、講談社学術文庫など。
⑥『古事記』:いっそのこと思いっきり古い方に針を振るのもアリかと。訳本各種あるが、三浦佑之訳(文春文庫)が手堅いか。
⑦同じラインで『風土記』。訳本いろいろ。全部は長いのでどこかの国をピックアップするか。
⑧渋沢栄一『論語と算盤』みぃはぁですが、次の一万円札の顔の人。日本の近代資本主義を作ったと言われる。ちくま新書に訳本あり。
⑨親鸞(述)・唯円著『歎異抄』:浄土真宗の祖、親鸞の言葉が収められた本。太平洋戦争時に戦地に持って行った学徒も多いらしい。訳本無数。
⑩世阿弥『風姿花伝』演劇論の古典。「秘すれば花」というフレーズのみ知られているが意外と読まれていない。訳本各種。
⑪二宮尊徳『二宮翁夜話』:ながら勉強の元祖のおじさん。疲弊した農村の改革に成功した二宮翁が残した教訓。訳本は中公クラシックスなど。
⑫レーニン『帝国主義』:ロシアを知るにはロシア革命の主役たるこの人の本も必読か。訳本いろいろ。
⑬和辻哲郎『風土』:京都学派の古典。比較文化論の名著。
⑭樋口一葉『にごりえ・たけくらべ』:たまには小説もよいかも。版元いろいろ。
以上です。ご連絡お待ちしております。

中江兆民『三酔人経綸問答』輪読会は昨日終了しました。ご参加の皆様、ありがとうございました。
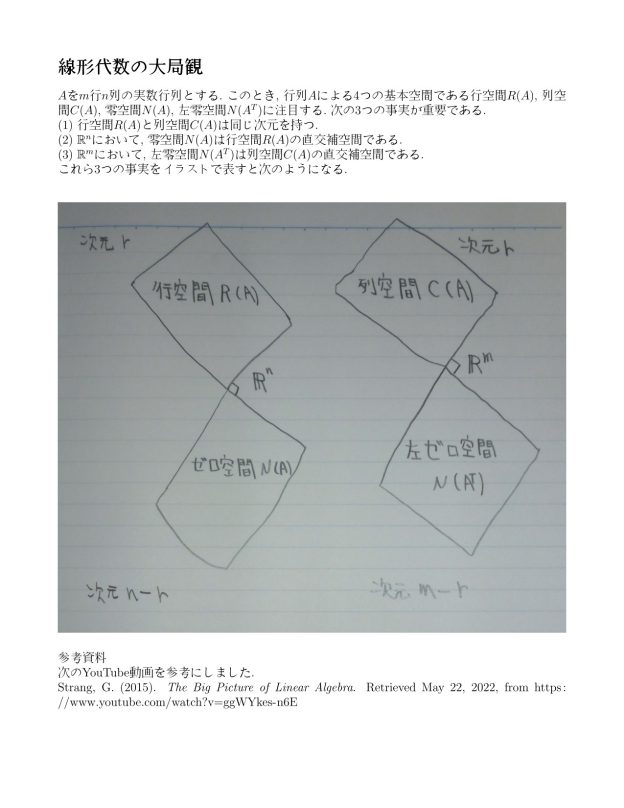
大学で学ぶ数学の分野に線形代数というものがあります。
線形代数を勉強したいのですが、範囲が広すぎて困りました。
そこで、線形代数の最重要ポイントをA4用紙1枚にまとめてみました。

作成: 藤原大樹
更新: 2022年5月22日