京都アカデメイアオンライン輪読会では、2月3日(金)20:00より、週1回のペースで世阿弥『風姿花伝』を読みます!
予習不要、どなたでも参加できます。ときどきの参加、一回だけのお試し参加も歓迎です。お問合せは kyotoacademeia@gmail.com まで。
なお、現代語訳の付いた本を各自でご用意ください。入手しやすいものを4つほど挙げておきますが、これら以外の本でも結構です。
多数のご参加をお待ちしています!


フリーランスの知人に依頼して、英語の音声教材を作成してもらいました。利点や今後の課題が見えてきたので、そのことについて執筆します。
私は趣味で英語の勉強をしています。塾に通っているわけではなく、完全に独学でやっています。最近は英単語力強化、いわゆるVocabulary Buildingに力を入れています。使用している英単語帳は「一杉武史著 改訂版 キクタン英検1級 アルク社」です。どうやって勉強するかというと、英単語帳の短いフレーズを何度も音読します。大学受験用のシステム英単語と同じ勉強方式です。さらに、リスニング力を向上させるには、自分で発音するだけでなく、音声教材のお手本を聴くことが重要です。ところが、キクタンでは長い例文の音声ファイルはありますが、短いフレーズには音声ファイルがありません。困ったことにリスニングの練習ができません。1つの解決策はネイティブスピーカーに依頼して音声教材を作成してもらうです。しかし、この方法はお金がかかり過ぎて無理です。2つ目の解決策は、人工知能を活用して音声教材を作るです。これは比較的安くできるのではないかと閃きました。
実はQuizletという無料のWebアプリがあります。Quizletは自作の単語カードを作って、Web上で暗記していくというシステムです。Quizletは単語カードを人工知能による音声で読み上げてくれます。しかし、英語の読み上げは少し不自然です。Quizletより自然な英語音声で勉強したいと思いました。
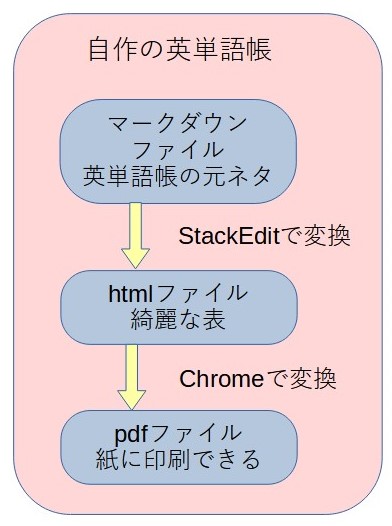
人工知能に英語を喋ってもらうためには、まず自作の英単語帳を作成する必要があります。今回はマークダウンファイルの表を用いて英単語帳を作ります。表の各行はフレーズを表します。そして表の各列は、ID番号、英語フレーズ、日本語フレーズ、コメントの4つです。マークダウンの実体はただのテキストファイルです。しかし、マークダウンは手軽に綺麗なドキュメントに変換できます。マークダウンファイルをhtmlファイルに変換することで綺麗な表ができます。その変換をするのはStackEditという無料のWebアプリです。次に、htmlファイルをPDFファイルに変換すれば、印刷できる状態になります。その変換をするのはChromeという無料のブラウザです。


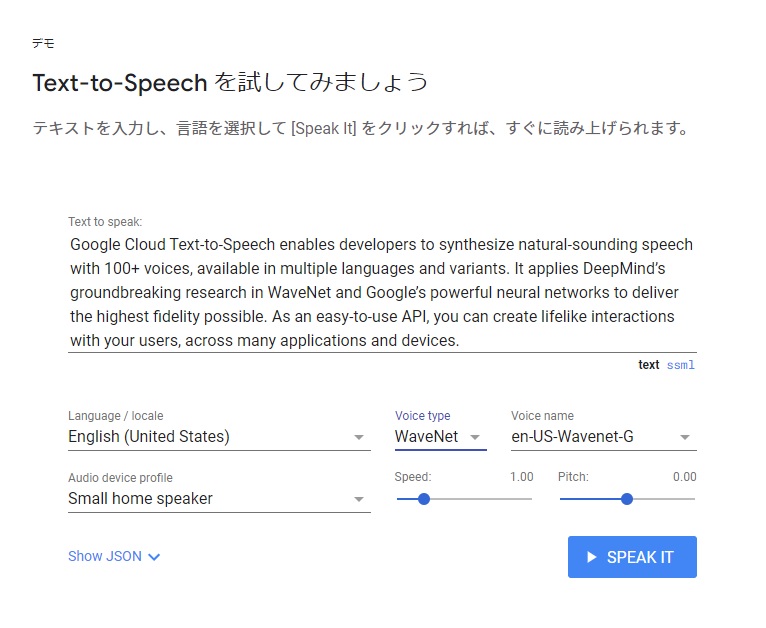
今回音声教材を作成するにあたって、Google社のWaveNetという人工知能を活用します。WaveNetはText-to-Speechという種類のソフトウェアで、文字情報を音声情報に変換してくれます。簡単にいうと原稿を読み上げるアナウンサーの役割を果たす人工知能です。高性能な人工知能なのですが、下記のサイトに無料の試用デモがあります。とりあえず、試用デモを動かして自分の好きな言葉をWaveNetに喋らせて下さい。音声が自然で人間に近いことが分かると思います。
https://cloud.google.com/text-to-speech
WaveNetは英語と日本語だけでなく、40以上の言語を喋ってくれます。そして、男女の声質が準備されています。利用料金は有料ですが、100万文字あたり$16米ドルで格安です。更に、最初の100万文字は毎月無料です。なので、英単語帳一冊分を読み上げるだけなら、実質無料で毎月利用できます。ただし、クレジットカード情報をGoogleに登録する必要があります。
必要な技術はプログラミング言語Pythonの入門レベルだけです。一般に、人工知能を活用するには高度な専門的知識が必要になります。しかし今回は、専門的知識は全く必要ありません。その理由は、WaveNetとPydubが直感的なPythonのAPIを提供してくれるからです。難しくはないが、時間と手間が掛かるという認識です。
Pythonプログラムを活用するに当たって、パソコン環境を整備する必要があります。以下の手順で行います。
Step1. 人工知能WaveNetを使える様にパソコン環境を整備する。
下記のYoutube動画を参考にします。
下記のPythonプログラムも参考になります。
https://gist.github.com/coding-youtuber/e8a2970bde14e08b5854fab5ae8003e4
Step2. PythonのライブラリPydubをインストールする。
Pydubは直感的なAPIで音声ファイルを連結できます。音声の連結は足算記号+で実現できます。
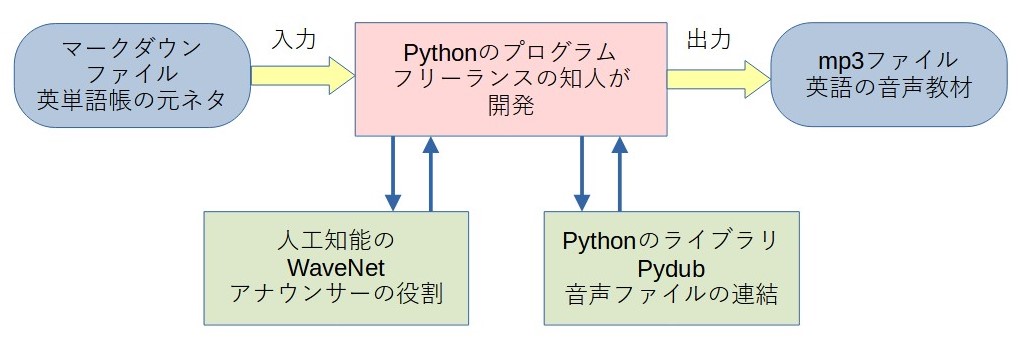
Pythonのプログラムを用いて音声教材を作成します。入力は英単語帳であるマークダウンファイルです。出力は音声教材であるmp3ファイルです。次の手順でPythonプログラムは動作します。
Step1.英語音声と日本語音声のそれぞれを作成する。
Step1.1 英語音声をWaveNetで作成する。
英語フレーズをアメリカ英語、Speed=0.85でmp3ファイルを作成する。
Speed=1.00は英語ネイティブの標準スピードなので速すぎます。Speed=0.85にすると少しゆっくり目で丁度良いです。
Step1.2 日本語音声をWaveNetで作成する。
日本語フレーズをSpeed=1.00でmp3ファイルを作成する。
日本語は標準スピードで問題ありません。
Step2. 英語音声と日本語音声を連結する。
Pydubを用いて英語と日本語のファイルを連結する。
1フレーズに対して、「英語から日本語へ」と「日本語から英語へ」の2種類のmp3ファイルを作成する。音声ファイルを連結する際に、下記の様に空白音声を入れる。
(英日ファイル) = (英語フレーズ) + (2秒間の空白) + (日本語フレーズ) + (2秒間の空白)。
(日英ファイル) = (日本語フレーズ) + (2秒間の空白) + (英語フレーズ) + (2秒間の空白)。
ファイル名は「ID番号.mp3」とする。
コメント列及びID番号列は読み上げない。
WaveNetは非常に賢い人工知能ですが、たまに漢字を誤読します。例を二つ挙げると、
例1:入力「口げんかはもう止(や)めなさい!」
=> WaveNet「口げんかはもう止(ど)めなさい!」
例2:入力「あなたの家までお供(とも)する」
=> WaveNet「あなたの家までお供(きょう)する」
などがあります。訓読みすべき漢字を音読みしてしまうという傾向があります。この問題は、入力をひらがなやカタカナにすることで取り敢えずは解決できます。例1だと、入力を「口げんかはもうやめなさい!」にするだけです。
実務上は次の手順で音声教材を改定します。
Step1. 音声ファイルを自分の耳で聴いて精密検査する。
Step2. 修正箇所の一覧表をマークダウン形式で作成する。
Step3. 修正箇所一覧表をPythonプログラムへ入力し、誤読のない音声ファイルを作成する。
Step4. 修正した音声ファイルで古い音声ファイルを上書きする。
Step5. 音声教材全体の最終検査をする。

さっそく音声教材を用いて英語のトレーニングをしてみました。リスニング力を向上させられそうな予感がしました。ほぼほぼ満足しています。日本語音声は少しだけ不自然です。将来的にGoogle社にWaveNetを改善してもらうしかないです。しかし不思議なもので不自然な音声でも数回聴くうちに耳が慣れます。日本語音声の不自然さは、仕方ないと諦めます。一方英語音声は、ネイティブ発音に完璧に近いと言える水準なので、大満足です。ただ、英語音声の方でも、少し怪しい発音を発見しました。例を挙げます。
“at the zenith of his career”と聴こえたでしょうか? 残念ながら私の耳にはそうは聴こえなかったです。聞き取り不可能でした。この現象は、私の英語耳が悪いのか、WaveNetが悪いのかは判断できません。したがって、英語音声についてもこれ以上の追求は行いません。
実は数年前に今回と同じように人工知能を用いて音声教材を作成しようとしました。その当時の合成音声技術は現在と比べてとても低かったです。非ネイティブの私が聴いても、英語音声は明らかに不自然でした。この数年間で技術の進歩があり、今回はGoogle社のWaveNetを利用することで、英語学習の実用に耐えうる音声教材を作成できました。
作成: 藤原大樹
更新: 2022年12月24日

言語哲学大全読書会は1巻を読了しました。次回1月27日(金)13時~16時に、趣向を大きく変え、クワインの『論理的観点から』所収「なにがあるのかについて」をとりあげます。会の名を分析哲学読書会と改めます。田島正樹先生と共に、分析哲学の骨組みを学びつくしましょう。引続き録画もご用意します。お問合せは kyotoacademeia@gmail.com まで。


正会員 藤原大樹です。
京都アカデメイアでは、以下の3つのイベントを同時並行で開催しています。
どのイベントも無料でどなたでも参加可能です。
皆様の御参加をお待ちしております。


正会員の藤原大樹です。
京アカの新しい企画イベントを練っています。突然ですが、以下の「京アカオンライン自習室」という企画を試験運用しようかと画策中です。皆様の御意見をお待ちしております。お問合せは kyotoacademeia@gmail.com まで。
私は趣味で英語を勉強しています。塾に通っているわけではなく、完全に独学でやってます。英語学習で大切なことは、とにもかくにも勉強を継続することです。独学のいいところは自分の気分が向いたときに、自分のレベル、スピードで学習できることです。独学の悪い所は、一度熱が冷めてしまうと、何もしない期間がどんどん長引いていく点です。このため継続ができなくなってしまう事が過去に多々ありました。独学だけど適度な緊張感を持って英語学習を継続する方法は何かないかと考えました。
一つの改善策は喫茶店でした。喫茶店では誰かに見られているかもしれないという気持ちが働くので集中力が少し向上しました。自宅だと自分以外だれもいないので、すぐダラケテしまいます。ただ喫茶店の欠点は、意外とお金がかかることです。スターバックス、コメダコーヒーの居心地は良いのですが、その分高いです。マクドナルドは安いけど、いつも混雑していて、勉強に集中しずらいです。自宅でもカフェと似たような環境をつくれないかと考えた結果、オンラインで誰かに見られているかも知れない環境を作れば良いと思いました。あまり良くない例えですが、フーコーのパノプティコンみたいなものです。対外的には、各自の好きなタイミングにオンラインでみんなで一緒に勉強するイベントです。
オンライン自習室の開催方法を具体化します。通常のオンライン勉強会では、指定テキストをみんなで一緒に読みます。けれど、京アカオンライン自習室では、勉強する内容は各自で準備します。各自がそれぞれのテキスト、レベル、スピードで勉強します。開催日時は事前に決めません。私が英語を勉強したいと感じた瞬間から、参加者をTwitterで募ります。つまり、ゲリラ開催です。開催日時を事前に決めない理由は、毎週△曜日△時と決めると、私の心理的負担が増大してしまうからです。場所はオンライン自習室のStudyverseを利用します。参加URLは毎回京アカのTwitterで通知します。参加費は完全無料です。参加資格は誰でもOKです。京アカ会員である必要はありません。顔出しNGの方は音声のみ、チャットのみの参加でかまいません。誰でも無料で参加できるイベントですが、注意してもらいたいことがあります。それは、オンライン自習室は原理的に世界中の人々から監視されているということです。参加者は各自、己の言動に細心の注意を払う必要があります。特にチャットへの書込みは慎重に行って下さい。チャットは文字として記録が残ります。つまり、後から見知らぬ誰かに閲覧される可能性が十分にあります。
本企画にはリスクがあります。誰もイベントに来ない可能性が高いです。別にそれでも構わないと私は思います。一人で勉強してても、誰か来るかもしれないという適度な緊張感を持てるからです。もう一つのリスクは、私のモチベーションです。私の勉強意欲が枯れてしまい、企画が中途半端に終わってしまう可能性も高いです。それでも本企画を試してみたいです。理想は、オンラインで緩い人間関係を構築し、ともに切磋琢磨しながら勉強していけたらいいなと思っています。

京都アカデメイアの泊昌史正会員が、静岡県舞台芸術センターの劇評コンクールで最優秀賞を受賞しました!
劇評本文は以下のリンクから読めます。演劇にご関心のある方は是非ご覧になってみてください。
公式
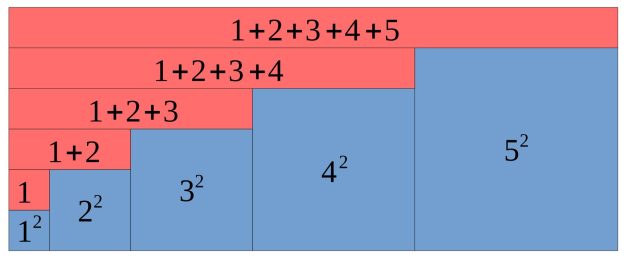
\[
1^2+2^2+3^2+ \dots + n^2 = \frac{1}{6}n(n+1)(2n+1)
\]
を4通りの方法で証明しました。
高校数学は奥が深いです。
そして更に、公式
\[
1^3+2^3+3^3+ \dots + n^3 = \frac{1}{4}n^2(n+1)^2
\]
を3通りの方法で証明しました。
作成: 藤原大樹
更新: 2022年8月17日

高校数学を復習しています。
公式
\[
1+2+3+ \dots + n = \frac{1}{2}n(n+1)
\]
を3通りの方法で証明しました。
作成: 藤原大樹
更新: 2022年8月9日
抜群に面白い入試問題を見つけたので、紹介します。ネイピア数$e$が無理数であること及び$e = \sum_{k=0}^\infty \frac{1}{k!}$であることの2つを証明します。入試問題なので高校数学しか使いませんし、問題の難易度はセンター試験レベルです。模範解答と問題解説をPDFファイルにまとめました。よかったら見て下さい。
作成: 藤原大樹
更新: 2022年8月6日

京アカオンライン輪読会では、次に和辻哲郎『風土―人間学的考察』(岩波文庫)の輪読会を、8月17日(水)20:00より始めます。前提知識一切不要、予習なしでその場で輪読し、議論します。試しに一回だけの参加、ときどきの参加もばっちりOK。どなたでも参加できます。参加ご希望の方は、各自で本をご用意下さい。お問合わせはkyotoacademeia@gmail.comまで。多数のご参加をお待ちしています!
https://www.iwanami.co.jp/book/b270343.html
