級数のオイラー変換について整理しました。既存のメルカトル級数及びライプニッツ級数にオイラー変換を適用すると、新たに興味深い級数が得られます。オイラーの着眼点が凄くて、本当に天才だなと感じました。
PDFファイル
作成: 藤原大樹
更新: 2025年12月1日

級数のオイラー変換について整理しました。既存のメルカトル級数及びライプニッツ級数にオイラー変換を適用すると、新たに興味深い級数が得られます。オイラーの着眼点が凄くて、本当に天才だなと感じました。
PDFファイル
作成: 藤原大樹
更新: 2025年12月1日
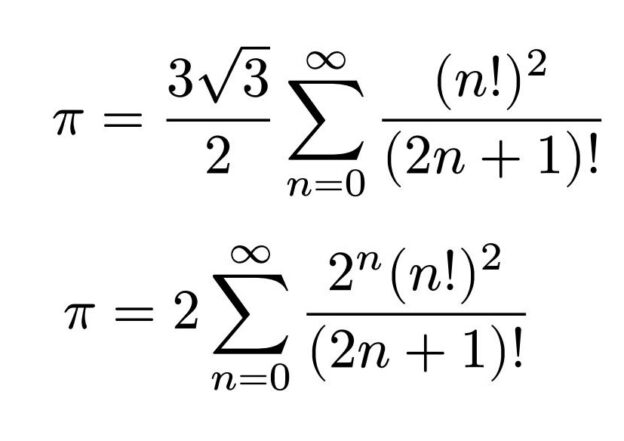
作成: 藤原大樹
更新: 2025年11月24日

京アカオンライン輪読会では『古事記』輪読会を11月15日(土)20:00より始めます。現代語訳は文春文庫の三浦佑之訳をはじめ沢山あります。どの訳でもいいので、各自でご用意ください。
どなたでも参加できます。お問合せは、京都アカデメイアkyotoacademeia@gmail.comまで!
参考までにいくつかURLを記しておきます。
文春文庫、三浦佑之訳(神代篇・人代篇)
講談社学術文庫、次田真幸訳(上下)
角川ソフィア文庫、中村啓信訳
河出文庫、池澤夏樹訳

ミル『自由論』の輪読会は11月1日に終了しました。ご参加下さった皆様、ありがとうございました。

京都アカデメイアオンライン輪読会では、8月9日(土)20:00よりJ.S.ミル『自由論』を読みます。どの訳でもよいので本は各自でご用意ください。
どなたでも、一回だけの参加でも歓迎です。お問合わせは京都アカデメイア kyotoacademeia@gmail.comまで!

原民喜『夏の花』輪読会は昨日で終了しました。ご参加下さった皆様、ありがとうございました。
次に読む本は改めて京アカMLその他で告知します。来週8月2日の輪読はお休みです。


柳田國男『明治大正史世相篇』オンライン輪読会は6月28日で終了しました。ご参加下さった皆様、ありがとうございました。
次に読む本は、あらためて京アカMLで告知いたします。
論理的思考力は、公教育、民間教育で非常に大切だとされています。
論理的思考力は、「なんにでも、どこででも使える」し、「ものごと、世界(社会)をみる・考える」ことは、これなくしては進められません。
考えることは、それ自体面白いですし、自在に考えることができる≪思考という自由≫を私たちに叶えてくれるのが、思考力、中でも論理的思考力です。
学校生・学生だけでなく、おとな、社会人が論理的思考力を培う(つちかう)ことで、仕事の資質ははるか、伸びるだろう。私のキャリアカウンセリングなどの経験からも感じますし、「学生、若手を育てる」には、まず論理的思考力だ、と思うばかりです。
「思考力を鍛える」 第一回のこの記事で取り組んでもらう「論理的思考」は、シンプルです。
■■■■■■■■■■■■■■■
≪今日の目標≫ 「二つの領域」を同時に考える「目を養う」
≪状況設定≫ あなたはいま、「目の前の課題」に着手するところです。
学校や大学の授業。朝からの業務。今日の家事。面談・相談の予定。
なんでも「一つ」、あなたの状況を思い浮かべて、設定してください。
あなたはいま、
A 目の前の課題 を見ていますね。
そのとき、
B それ以外のこと/周辺のこと/背景となること/Aのベース(基盤)となっているもの…
このBの視野を持つことはできますか。
「A 目の前の課題」を見据えると同時に、
「B それ以外のこと/周辺のこと/背景となること/Aのベース(基盤)となっているもの…」、つまり、課題Aの「周辺」「背景」「ベース(基盤)」「これまでの経緯」はなんだろうと、一つひとつ、設定した状況から、具体的にあげてみましょう。
手書きが早いのですが、自信があれば、頭の中の作業でも結構です。
図で描けば、「Aの外縁やもっと外、また背後、基盤部分が、Bである」。これが見えますね。
実際、「A 目の前のこと」には、このBが必ず伴う。BあってこそのAですよね。
■■■何が見えましたか?■■■
あなたが描いたBは、どんな様子をしていますか=明瞭な区分けができた図でなくてよい。
「Aの外縁=ぎりぎり『A 目の前の課題』に入ること」も、あるだろうか。
■■■明瞭な「論理構造」でなくても良い(現実社会では、「はっきりと区分けできない」「なんとも言えない混濁」がある)■■■
これは、ふだんの生活で、いつも当たり前にやっておられることですね。
≪例≫ A 今日は、朝一のルーティン(始業前後の流れ)をこなして、すぐにお客様Tにご連絡をとり、大事な日程の延期の旨を伝えて、おわび。日程を再調整する。ご連絡方法は、まずはお電話にて。訪問で出ておられる可能性が高いが、手順として。
書き出すと、長いな… 「目の前の一個の課題」とはいえ、あなたの分野、生活をよく知る方ではなく、社会一般の方が理解できそうな説明で課題を書き表すと、結構手間がかかるんですよね。
また、「目の前の課題」は、「十分な慣れと洗練がある」あなたは、本当は(こんな説明では足りず)「もっと細かい色々が要る」と、感じるはず(下の【参考1】へ)。
■■■「ふだんの慣れ、洗練」を考える哲学へ■■■
【参考1】京都アカデメイアblog 筆者・後藤敦子の前記事
「皆とちがう子」。天分を知ること。天分は職業にできるのか
記事の最後、小林秀雄の講演録からの引用(小林秀雄『人生について』中公文庫、1978年(2019年改版)、10頁)をご参照ください。
仕事や学業には、自分にしかわからない、自分だから伸ばせたやり方がある。ちょっとした加減。「B 周辺、背景…」をどの程度、前提として頭に入れておくか。Bを頭から排除し、いまAだけを考えるのも、やり方だ。「あなたがやってきた熟練」を平たく説明するのは、「無理だよ。人には、わからない」と、あなたはご存知でしょう= これは、現象学など哲学でも言われることです。
■■■■■■■■■■
さて、B でぱっと書きだした(頭の中で、書き出せた)ことが、どんな様子をしているか。
この問題に戻りましょう。
「B Aの周辺…」は、上のAの例を表現するのに、これだけの説明を要しましたので、私からは具体的な例示を省略。
それより、今日、考えてもらいたいのは、
B をどう「定義」するか。どう「言い表す」か です。
■■■あるものをどう「定義」「表現」するか、という問題■■■
●Aの「外縁」 …Aに含まれているが、その縁(ふち)、外縁に位置すること。
●Aの「周辺」…「周りが見えているかどうか」。
●Aの「背景」…背景とは、なんだろう。何を「背景」と呼びますか(言い表しますか)。
例1: Aを行う「理由」「経緯」。なぜそれをするのか。背景事情。
例2:Aを行うとき、背景Bは意識する必要がありますか。慣れた実施者なら、背景Bはいつでも見えている、いえ、背景Bのほうが「目の前のAが上手くできるか」より、重要だ、と考える場合もあるでしょうね。行為Aの背景(Aの環境や、Aが必要な状況)と、Aの行為者の背景(行為者のこれまで。経験など)。どちらも背景とは呼べる。
□□□【「背景」の例】テストと学力の相関□□□
目の前に迫ったテスト(=A)は、直前の詰め込み勉強で良い点数が取れたが、
学力そのもの(=B)がつかなかったのであれば、Aの結果より、Bの「学力」のほうが大事だといえますね。
□□□□□□□□□
●Aの「ベース(基盤)」とは…
例1:Aを行う基礎として、B1,B2… の能力がなければならない。
例2:安心、安定してAが行えるのは、B1,B2… の基盤(や保障)があるからだ。通常は、この基盤(保障)は問題とならないが、「何かあったときは」基盤(保障)の確かさが問われる。
■■■■■■■■■■
はい、ここまで。
Bについては、私は抽象的な説明で通しましたが、上の表現で「こんなことかな」と、逐一、理解できましたか。AとB、たった二つを述べる・描くだけで、思考はいつまでも続けられそうだし、「あなたにはわかっていることを、改めて説明の形にする労苦」「私が抽象化した内容を、文字で理解する」、これに疲れますよね。慣れやセンスをすでに磨いた方は、すらすら読めて、私が今日は指摘しなかった「AとBの関係性の妙(不思議な連関)」や、他の重要な論点ですぐに語れるでしょう。
□□□□□□□□□□
この「思考の練習」で、もう少し、大事な観点を加えておきましょう。
●「Aの後」、また「もっと長いスパンで」行為者であるあなたは、この先が見えている必要がありますよね。後先考えずに、やれない ≪未来への視野、準備≫
●Bで挙げた中に、あなたの「得意な視野・視点」、「得意ではないが、あることはわかっている視野・視点」があったと思います。
では、あなたに見えたBの、さらに「周辺」「外」「基盤」「未来」…
これは、どれくらいあると考えますか ≪あなたの視野・視点をこえた範囲が、おそらくあること≫ …思考の主義によっては、「そこまでは考えない」とされてもよい。切りがないことに、思いを向けるかどうか。毎日の勉強や仕事、家事も、「切りがない」と、「切りをつける」。
□□□□□□□□□□
はい、戻って。Bを「定義する」「表現する(言い表す)」ことが、なぜ重要か。
論点1:どれくらいの抽象度で「定義」するか ≪これと特定できない、抽象度の高い定義にすると、さまざまな事象について、この定義でBを説明できます(汎用性が高い)≫
論点2:Bの「表現のしかた」「言い表し方」によって、Bの内容が変わる。同じことを、どう「表現するか」によって、Bの意味も変わる場合がある。「どう定義、表現するかで、指し示す内容や意味は変わる」ことを、どこかで感じた経験はありますか(下の【参考2】へ)。
論点3:Bの定義だけでなく、Aの「目の前のこと」を「どう言い表すか」「どう位置づけているか」。Aも、表現や位置づけによって、意味が変わると気づけますね。
□□□blog前記事の「読みを深める」思考、観点へ□□□
【参考2】京都アカデメイアblog 筆者・後藤敦子の前記事
「皆とちがう子」。天分を知ること。天分は職業にできるのか
この記事では、「皆とちがう子」といった表現で、精神病理学概念 Anderssein((【独(ドイツ語)】アンダーセイン;ちがっていること)を考えました。
「ぼくは、みんなから、はずれてる。みんなのようではない」と、疎外に悲しむ子。
もし、「ぼく」のあり方(態様)に異なる表現が与えられていたら(「ぼく」が表現を変えることができたら)。「ちがっていること」Anderssein の意味は変わるかもしれません。
精神医学・精神病理学、心理学で、このように、「表現のしかた次第で、彼の(患者・CL(クライエントの)くるしみは、変わるのではないか」と考える観点は、あちこちで出されました。これには膨大な研究、臨床実践があり、特定の立場や研究の紹介、また諸研究をふまえての「私の見解」を今日はお話できませんが(いずれ、紹介しますね)。
「この表現は、もっとちがう表現にできるものなのだろうか。本質的に」。
この視点から読むと、「ぼくは、皆とちがう。いつも、みんなの中でのんきに居ることができなかった」ーここへの「読みが深まる」はずです ≪読む力の醸成≫
□□□□□□□□□
■■■一歩すすんで 今日、最も得てもらいたかった思考へ■■■
最後に、一歩すすみます。今日、私たちはどんな「思考」に近づいたのか。
総括しつつ、ブログ前記事(「皆とちがう子」。天分を知ること。天分は職業にできるのか)を題材に、解説しますね。
この前記事で、筆者の私があえて、あのような表現形態(当事者の切実な疎外をていねいに伝える書き方、文体)をとった理由。なぜ私は、「ぼくのAnderssein」に「根源的エッセイを試みた」のでしょうか。「ぼくのAnderssein」は、「あなたの目の前にあらわれた言葉(現象)A」ですね。これを私が前面に出した(めだたせた)背景、意図は、なんだと思いますか。
(実は、私の「書き方、伝え方」には、専門的な(精神病理学上の)意図があったのです)
≪見えているもの(言葉、現象)だけを見るのではなく ”より自由な、一歩引いた態度で”「そのとき、筆者の私が考えていたこと」を考えてみる。この「複眼思考」を「自然と使える」≫ ことに慣れていきましょう(前記事で、私が「何を考え、意図したのか」は、こんどお話しますね)。
思考力、論理的思考では、こうして
”より自由な、一歩引いた態度で”
” 複眼的に、ゆったりと考える”
≪自分を自由にできる思考態度≫ が、かぎとなります。
■■■■■まとめ 目を養う 目と思考■■■■■
さて、今日は、AとBを「同時に見る」ことから始めて、より高度な思考、
≪一歩引いた態度で、複眼思考を自由にすすめる≫≪目を養う≫≪読む力の醸成≫
ここまで到達できましたね。
「目を養う」のは「思考を育てる」ことですね。
あなたは、≪まるで目、視覚機能を使うようにして≫「思い描き」「より高次の思考にすすんだ」でしょう? これも、思考の要です。
目の前のAに取りかかるのだが、そのとき、どこかをゆったりと見つめる・考えている。こんなゆとりある視野、思考を仕事や学業、忙しい日常で営めると、「Aをやらなきゃならない」、この意味ややり方も、変わってくるでしょう。
「なんとなく、わかった」かな。一記事の分量で解説するには、抽象論でざっと話す部分が必要で、この私の文章を読みこなせるかが、関門となった方がいると思います。
□□□「論理的思考と言うけど、あちこち、行きつ戻りつ、余剰が話され… 話の全体像を描けなかったぞ!」□□□
そのとおり。このたねあかしは、次回。お疲れさま!
■■■■■■■■■■
後藤敦子… 教育学士(京都大学)、臨床哲学(文学)修士(大阪大学・院)。キャリアコンサルタント、産業カウンセラー、介護諸資格。福祉介護職、団体代表、世界遺産・高野山の飲食店再建。長く不登校、ひきこもり支援に携わり、公的事業運営・個人事業。臨床はじめ仕事の基盤は、いまも京大以来の現象学(哲学)、精神病理学。現在はさまざま兼業: 国土交通省事業カウンセラー(警察庁方式 運転適性検査・指導者/独立行政法人自動車事故対策機構 第一種カウンセラー)、国家公務員のカウンセラー、病院での患者さま接遇。夜間中学校教育にも心を寄せる。
#思考力を鍛える #論理的思考力 #学力形成論 #思考という自由 #目を養う #社会人の資質向上 #あたりまえの哲学 #定義 #表現の可能性 #意味の変容 #疎外 #孤独 #筆者の意図 #深い読み方 #複眼思考 #自由な態度 #ゆったりと見つめる #思い描く力 #視覚と思考 #現象学 #哲学 #精神病理学 #京都アカデメイア #後藤敦子 #和歌山